题目内容
1.实数x,y满足$\left\{\begin{array}{l}{y≤2x+2}\\{x+y-2≥0}\\{x≤2}\end{array}\right.$,则z=|x-y|的最大值是( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 根据题意,作出不等式组$\left\{\begin{array}{l}{y≤2x+2}\\{x+y-2≥0}\\{x≤2}\end{array}\right.$的可行域,令m=y-x,分析可得m的取值范围,而z=|x-y|=|m|,分析可得z的最大值,即可得答案.
解答  解:依题画出可行域如图,可见△ABC及内部区域为可行域,
解:依题画出可行域如图,可见△ABC及内部区域为可行域,
令m=y-x,则m为直线l:y=x+m在y轴上的截距,
由图知在点A(2,6)处m取最大值是4,在C(2,0)处最小值是-2,
所以m∈[-2,4],
而z=|x-y|=|m|,
所以z的最大值是4,
故选:B.
点评 本题考查线性规划求不等式的最值问题,关键是正确作出不等式的可行域.

练习册系列答案
相关题目
12.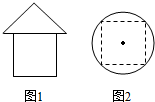 一个几何体的三视图如图所示,其中图1为正视图和侧视图(三角形为等腰直角三角形,四边形为边长为2的正方形),图2为俯视图(正方形为圆内接正方形),则这个几何体的表面积为( )
一个几何体的三视图如图所示,其中图1为正视图和侧视图(三角形为等腰直角三角形,四边形为边长为2的正方形),图2为俯视图(正方形为圆内接正方形),则这个几何体的表面积为( )
 一个几何体的三视图如图所示,其中图1为正视图和侧视图(三角形为等腰直角三角形,四边形为边长为2的正方形),图2为俯视图(正方形为圆内接正方形),则这个几何体的表面积为( )
一个几何体的三视图如图所示,其中图1为正视图和侧视图(三角形为等腰直角三角形,四边形为边长为2的正方形),图2为俯视图(正方形为圆内接正方形),则这个几何体的表面积为( )| A. | $2\sqrt{2}π+20$ | B. | $\frac{{2\sqrt{2}π}}{3}+8$ | C. | $({2\sqrt{2}+2})π+16$ | D. | $2\sqrt{2}π+16$ |
9.设集合A={x|x2-3x-4>0},集合B={x|-2<x<5},则A∩B=( )
| A. | {x|-1<x<4} | B. | {x|-2<x<-1或4<x<5} | C. | {x|x<-1或x>4} | D. | {x|-2<x<5} |
6.已知抛物线y2=4x的焦点为F,A、B为抛物线上两点,若$\overrightarrow{AF}=3\overrightarrow{FB}$,O为坐标原点,则△AOB的面积为( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{8\sqrt{3}}}{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
13.已知直角梯形ABCD,AD∥BC,∠BAD=90°.AD=2,BC=1,P是腰AB上的动点,则$|\overrightarrow{PC}+\overrightarrow{PD}|$的最小值为3.
11.已知函数f(x)=sin(2x-$\frac{π}{2}$)(x∈R)下列结论错误的是( )
| A. | 函数f(x)的最小正周期为π | B. | 函数f(x)是偶函数 | ||
| C. | 函数f(x)在区间[0,$\frac{π}{2}$]上是增函数 | D. | 函数f(x)的图象关于直线x=$\frac{π}{4}$对称 |
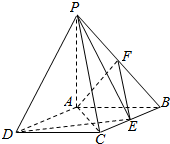 如图:四棱锥P-ABCD中,底面ABCD是平行四边形,且AC=BD,PA⊥底面ABCD,PA=AB=1,$BC=\sqrt{3}$,点F是PB的中点,点E在边BC上移动.
如图:四棱锥P-ABCD中,底面ABCD是平行四边形,且AC=BD,PA⊥底面ABCD,PA=AB=1,$BC=\sqrt{3}$,点F是PB的中点,点E在边BC上移动.