题目内容

17．已知（a2+2a+3）x＞（a2+2a+3）1-x，求x的取值范围．

分析 先判断底数大于1，再根据指数函数的单调性可得x＞1-x，从而求得x的范围．

解答 解：∵a2+2a+3=（a+1）2+2＞1，（a2+2a+3）x＞（a2+2a+3）1-x，
∴x＞1-x，求得x＞$\frac{1}{2}$，故x的取值范围为（$\frac{1}{2}$，+∞）．

点评 本题主要考查指数函数的单调性，指数不等式的解法，判断底数大于1，是解题的关键，属于基础题．

练习册系列答案
相关题目
7．定义运算：x▽y=$\left\{\begin{array}{l}{x（xy≥0）}\\{y（xy＜0）}\end{array}\right.$，例如：3▽4=3，（-2）▽4=4，则函数f（x）=x2▽（2x-x2）的最大值为（　　）
A．0B．1C．2D．4
8．求函数y=$\sqrt{3tanx+\sqrt{3}}$的定义域．
5．已知抛物线C的方程为x2=2py（p＞0），过点M作抛物线C的两条切线，切点分别为A，B（A右B左）．
（1）若点M的坐标为（1，-$\frac{3}{2}$），一个切点B的横坐标为-1，求抛物线C的方程；
（2）若点M的坐标为（a，-2p）（a为常数），设直线AM，BM的斜率分别为k1，k2，求证：k1•k2为定值．
12．函数g（x）=lg（x-$\frac{1}{x}$）的图象是（　　）
A．B．C．D．
2．若函数f（x）在定义域D内的某个区间I上是增函数，且F（x）=$\frac{f（x）}{x}$在I上也是增函数，则称y=f（x）是I上的“完美增函数”．已知f（x）=ex+x，g（x）=lnx-1．
（1）判断函数f（x）是否为区间（0，+∞）上的“完美增函数”；
（2）若函数g（x）是区（0，m]上的“完美增函数”，求整数m的最大值．
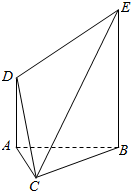3．如图，△ABC为等边三角形，D，E是平面ABC同一侧的两点，DA⊥平面ABC，EB⊥平面ABC，EB=2DA．
（Ⅰ）求证：平面EDC⊥平面EBC；
（Ⅱ）若∠EDC=90°，求直线EB与平面EC所成角的正弦值．
20．某三棱锥的三视图如图所示，则该几何体的体积为$\frac{4}{3}$．
1．实数x，y满足$\left\{\begin{array}{l}{y≤2x+2}\\{x+y-2≥0}\\{x≤2}\end{array}\right.$，则z=|x-y|的最大值是（　　）
A．2B．4C．6D．8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网