题目内容
18.已知各项不为0的等差数列{an}满足a4-2a${\;}_{7}^{2}$+3a8=0,数列{bn}是等比数列,且b7=a7,则b3b8b10=( )| A. | 1 | B. | 8 | C. | 4 | D. | 2 |
分析 利用等差数列通项公式先求出b7=a7=2,再由等比数列性质能求出b3b8b10的值.
解答 解:设等差数列的公差是d,
∵a4-2a${\;}_{7}^{2}$+3a8=0,
∴${a}_{7}-3d-2{{a}_{7}}^{2}+3({a}_{7}+d)=0$,
解得a7=2或a7=0,
∵各项不为0的等差数列{an},
∴舍去a7=0,
∵数列{bn}是等比数列,且b7=a7,∴b7=2,
∴b3b8b10=(b7)3=8.
故选:B.
点评 本题考查等差数列、等比数列性质的应用,是基础题,解题时要认真审题,注意等差数列的通项公式的合理运用.

练习册系列答案
相关题目
15.计算[(-$\sqrt{2}$)2]-$\frac{1}{2}$的结果是( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
8.在△ABC中,∠C=60°,AC=2,BC=3,那么AB等于( )
| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | $\sqrt{7}$ | D. | $2\sqrt{2}$ |
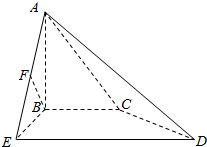 如图,四棱锥A-BCDE中,AB、BC、BE两两垂直且AB=BC=BE,DE∥BC,DE=2BC,F是AE的中点.
如图,四棱锥A-BCDE中,AB、BC、BE两两垂直且AB=BC=BE,DE∥BC,DE=2BC,F是AE的中点.