题目内容
9.已知各项均为正数的数列{an}的前n项和Sn满足8Sn=a${\;}_{n}^{2}$+4an+3(∈N*),且a1<3.(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=$\frac{{a}_{n}+3-3n}{{2}^{n-1}}$,设{bn}的前n项和为Tn,若不等式(-1)nλ<Tn+$\frac{n}{{2}^{n-1}}$对一切n∈N*恒成立,求实数λ的取值范围.
分析 (1)利用递推关系与等差数列的通项公式即可得出;
(2)利用“错位相减法”与等比数列的前n项和公式可得Tn,对n分类讨论即可得出.
解答 解:(1)∵$8{S_n}={a_n}^2+4{a_n}+3$,
∴8Sn-1=${a}_{n-1}^{2}$+4an-1+3 (n≥2),
∴$8({S_n}-{S_{n-1}})={a_n}^2+4{a_n}-{a^2}_{n-1}-4{a_{n-1}}$,
∴${a_n}^2-{a^2}_{n-1}=4({a_n}+{a_{n-1}})$,
∵an>0,∴an-an-1=4(n≥2).
∴数列{an}是以4为公差的等差数列,
又∵$8{S_1}={a_1}^2+4{a_1}+3$,
∴${a_1}^2-4{a_1}+3=0$而a1<3,
∴a1=1,
∴an=4n-3 (n∈N*).
(2)${b_n}=\frac{n}{{{2^{n-1}}}}$,
${T_n}=1×\frac{1}{2^0}+2×\frac{1}{2^1}+3×\frac{1}{2^2}+…+(n-1)×\frac{1}{{{2^{n-2}}}}+n×\frac{1}{{{2^{n-1}}}}$,
$\frac{{T}_{n}}{2}$=$\frac{1}{2}+2×\frac{1}{{2}^{2}}$+…+$(n-1)×\frac{1}{{2}^{n-1}}$+n×$\frac{1}{{2}^{n}}$,
两式相减得$\frac{T_n}{2}=\frac{1}{2^0}+\frac{1}{2^1}+\frac{1}{2^2}+…+\frac{1}{{{2^{n-1}}}}-n×\frac{1}{2^n}=2-\frac{n+2}{2^n}$,
∴${T_n}=4-\frac{n+2}{{{2^{n-1}}}}$,
∴${(-1)^n}λ<4-\frac{2}{{{2^{n-1}}}}$.
若n为偶数,则$λ<4-\frac{2}{{{2^{n-1}}}},{\;}∴λ<3$.
若n为奇数,则$-λ<4-\frac{2}{{{2^{n-1}}}}$,∴-λ<2,∴λ>-2.
∴-2<λ<3.
点评 本题考查了递推关系、等差数列与等比数列的通项公式及其前n项和公式、分类讨论方法,考查了推理能力与计算能力,属于中档题.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案| A. | 2015 | B. | 2016 | C. | 4030 | D. | 4032 |
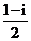 .
.