题目内容
关于x的一元二次方程mx2-(1-m)x+m=0没有实数根,则实数m的取值范围是 .
考点:一元二次方程的根的分布与系数的关系
专题:计算题,不等式的解法及应用
分析:由题意可得它的判别式△=(1-m)2-4m•m<0,且m≠0,由此求得m的取值范围.
解答:
解:由于关于x的一元二次方程mx2-(1-m)x+m=0没有实数根,
故它的判别式△=(1-m)2-4m•m<0,且m≠0,
求得m>
或m<-1,
故m的范围为(-∞,-1)∪(
,+∞).
故答案为:(-∞,-1)∪(
,+∞).
故它的判别式△=(1-m)2-4m•m<0,且m≠0,
求得m>
| 1 |
| 3 |
故m的范围为(-∞,-1)∪(
| 1 |
| 3 |
故答案为:(-∞,-1)∪(
| 1 |
| 3 |
点评:本题主要考查一元二次方程根的分布情况,考查运算能力,属于基础题.

练习册系列答案
相关题目
若关于x的不等式cosθ(1-x)2-2x(1-x)+2
x2sinθ≥0对一切x∈[0,1]恒成立,则θ的取值范围是( )
| 2 |
A、[kπ+
| ||||
B、[2kπ+
| ||||
C、[kπ+
| ||||
D、[2kπ+
|
如图,PA垂直于正方形ABCD所在平面,则以下关系错误的是( )
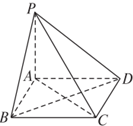

| A、平面PCD⊥平面PAD |
| B、平面PCD⊥平面PBC |
| C、平面PAB⊥平面PBC |
| D、平面PAB⊥平面PAD |
双曲线
-
=1的离心率e∈(1,2),则实数k的取值范围是( )
| x2 |
| 4 |
| y2 |
| k |
| A、(0,4) | ||
| B、(1,1) | ||
C、(0,2
| ||
| D、(0,12) |
在正方体ABCD-A1B1C1D1中,下列各 式运算结果为向量
的是( )
①(
-
)-
;
②(
+
)-
;
③(
-
)-
;
④(
-
)+
.
| BD1 |
①(
| A1D1 |
| A1A |
| AB |
②(
| BC |
| BB1 |
| D1C1 |
③(
| AD |
| AB |
| DD1 |
④(
| B1D1 |
| A1A |
| DD1 |
| A、①② | B、②③ | C、③④ | D、①④ |
函数f(x)=1-log3x的零点是( )
| A、(1,1) | B、1 |
| C、(3,0) | D、3 |
 已知函数f(x)=
已知函数f(x)=