题目内容
已知m,n为正数,实数x,y满足
x+
y-3
-3
=0,若x+y的最大值为27,则m+n= .
| 2 |
| 2 |
| x+m |
| y+n |
考点:函数的最值及其几何意义
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:由题意,
+
=
,从而得到
≥(
)2,令x+y=u,则u2-9u-9(m+n)≤0,从而得27是方程u2-9u-9(m+n)=0的解,从而求解.
| x+m |
| y+n |
| ||
| 3 |
| x+y+m+n |
| 2 |
| ||
| 6 |
解答:
解:由题意,
+
=
,
则
(
+
)=
•
,
则由
≥(
)2可得,
≥(
)2,
令x+y=u,
则上式可化为
u2-9u-9(m+n)≤0,
又∵u=x+y的最大值为27可知,
27是方程u2-9u-9(m+n)=0的解,
即27×27-9×27-9(m+n)=0,
解得m+n=27×2=54,
故答案为:54.
| x+m |
| y+n |
| ||
| 3 |
则
| 1 |
| 2 |
| x+m |
| y+n |
| 1 |
| 2 |
| ||
| 3 |
则由
| x+y+m+n |
| 2 |
| ||||
| 2 |
| x+y+m+n |
| 2 |
| ||
| 6 |
令x+y=u,
则上式可化为
u2-9u-9(m+n)≤0,
又∵u=x+y的最大值为27可知,
27是方程u2-9u-9(m+n)=0的解,
即27×27-9×27-9(m+n)=0,
解得m+n=27×2=54,
故答案为:54.
点评:本题考查了基本不等式的应用及不等式与方程的解的关系,属于中档题.

练习册系列答案
相关题目
定义函数f(x)=
,则函数g(x)=xf(x)-6在区间[1,64]内所有的零点的和为( )
|
| A、192 | ||
| B、189 | ||
C、
| ||
D、
|
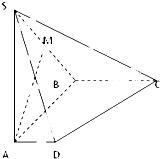 如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,AD∥BC,∠ABC=90°,SA=AB=BC=2,AD=1.M是棱SB的中点.
如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,AD∥BC,∠ABC=90°,SA=AB=BC=2,AD=1.M是棱SB的中点. 如图,AB是圆O的直径,C是圆O上的点.P是圆所在的面外一点.设Q为PA的中点,G为AOC的重心.求证:QG∥平面PBC.
如图,AB是圆O的直径,C是圆O上的点.P是圆所在的面外一点.设Q为PA的中点,G为AOC的重心.求证:QG∥平面PBC.