题目内容

化简：tanα（cosα-sinα）+
sinα(sinα+tanα)
1+cosα
．
考点：三角函数的化简求值
专题：三角函数的求值
分析：运用同角的三角函数关系式化简即可．
解答： 解：tanα（cosα-sinα）+
sinα(sinα+tanα)
1+cosα

=sinα-
sin2α
cosα
+
sin2α+
sin2α
cosα
1+cosα

=sinα-
sin2α
cosα
+
sin2α
cosα

=sinα．
点评：本题主要考察了三角函数的化简求值，属于基础题．
练习册系列答案
相关题目
已知全集U={1，2，3，4，5}，A={1，3，5}，则∁UA=（　　）
A、{1，2}
B、{2，4，5}
C、{2，3，4}
D、{2，4}
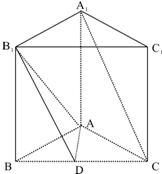如图，底面是正三角形的直三棱柱ABC-A1B1C1中，D是BC的中点，AA1=AB=2．
（1）求证：A1C∥平面AB1D；
（2）求三棱锥A1一AB1D的体积．
已知中心在原点，焦点在坐标轴上的椭圆与直线x+y=1交于A、B两点，M为AB的中点，直线OM（O为原点）的斜率为
2
2
，且OA⊥OB，求椭圆的方程．
两圆x2+y2+2x-4y+3=0与x2+y2-4x+2y+3=0上的点之间的最短距离是
 
．
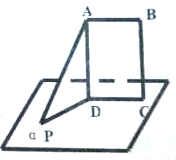如图，已知AB∥α，AD⊥α，BC⊥α，垂足为D、C，PA⊥AB，求证：CD⊥平面PAD．
已知m，n为正数，实数x，y满足
2
x+
2
y-3
x+m
-3
y+n
=0，若x+y的最大值为27，则m+n=
 
．
已知f（x）=
sinθ
3
x3+
3
2
cosθ•x2，θ∈[0，
5π
12
]，则f′（1）取值范围为
 
．
直线ax+by=ab（a＞0，b＜0）的倾斜角是（　　）
A、arctan(-
a
b
)
B、arctan
a
b
C、π-arctan
a
b
D、
π
2
+arctan
a
b

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网