题目内容
定义函数f(x)=
,则函数g(x)=xf(x)-6在区间[1,64]内所有的零点的和为( )
|
| A、192 | ||
| B、189 | ||
C、
| ||
D、
|
考点:函数零点的判定定理
专题:函数的性质及应用
分析:函数f(x)是分段函数,要分区间进行讨论,当1≤x≤2,f(x)是二次函数,当x>2时,对应的函数很复杂,找出其中的规律,最后作和求出
解答:
解:当1≤x≤
时,f(x)=8x-8,
所以g(x)=8(x-
)2-8,此时当x=
时,g(x)max=0;
当
≤x≤2时,f(x)=16-8x,所以g(x)=-8(x-1)2+2<0;
由此可得1≤x≤2时,g(x)max=0,
∴函数g(x)在区间[1,2]上只有一个零点
;
下面考虑2n-1≤x≤2n且n≥2时,g(x)的最大值的情况:
当2n-1≤x≤3•2n-2时,由函数f(x)的定义知f(x)=
f(
)=
f(
)=…=
f(
),
因为1≤
≤
,
所以g(x)=
(x-2n-2)2-8,
此时当x=3•2n-2时,g(x)max=0;
当3•2n-2≤x≤2n时,同理可知,g(x)=-
(x-2n-1)2+8<0.
由此可得2n-1≤x≤2n且n≥2时,g(x)max=0,函数只有一个零点.
综上可得:对于一切的n∈N*,函数g(x)在区间[2n-1,2n]上有1个零点,
从而g(x)在区间[1,2n]上有n个零点,且这些零点为xn=3•2n-2,因此,所有这些零点的和为
(2n-1).
∵64=26
∴所有这些零点的和为
(2n-1)=
(26-1)=
.
故选:D.
| 3 |
| 2 |
所以g(x)=8(x-
| 1 |
| 2 |
| 3 |
| 2 |
当
| 3 |
| 2 |
由此可得1≤x≤2时,g(x)max=0,
∴函数g(x)在区间[1,2]上只有一个零点
| 3 |
| 2 |
下面考虑2n-1≤x≤2n且n≥2时,g(x)的最大值的情况:
当2n-1≤x≤3•2n-2时,由函数f(x)的定义知f(x)=
| 1 |
| 2 |
| x |
| 2 |
| 1 |
| 22 |
| x |
| 22 |
| 1 |
| 2n-1 |
| x |
| 2n-1 |
因为1≤
| x |
| 2n-1 |
| 3 |
| 2 |
所以g(x)=
| 1 |
| 22n-5 |
此时当x=3•2n-2时,g(x)max=0;
当3•2n-2≤x≤2n时,同理可知,g(x)=-
| 1 |
| 22n-5 |
由此可得2n-1≤x≤2n且n≥2时,g(x)max=0,函数只有一个零点.
综上可得:对于一切的n∈N*,函数g(x)在区间[2n-1,2n]上有1个零点,
从而g(x)在区间[1,2n]上有n个零点,且这些零点为xn=3•2n-2,因此,所有这些零点的和为
| 3 |
| 2 |
∵64=26
∴所有这些零点的和为
| 3 |
| 2 |
| 3 |
| 2 |
| 189 |
| 2 |
故选:D.
点评:本题主要考查了根的存在性及根的个数的判断的问题,是一道较复杂的问题,首先它是分段函数,各区间上的函数又很复杂,挑战人的思维和耐心.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
已知函数f(x)=
,若f(x)=x+a有且只有两个不相等的实数根,则实数a的取值范围是( )
|
| A、(-∞,0] |
| B、(-∞,0) |
| C、[0,1) |
| D、[0,+∞) |
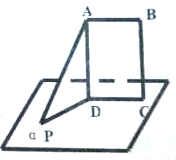 如图,已知AB∥α,AD⊥α,BC⊥α,垂足为D、C,PA⊥AB,求证:CD⊥平面PAD.
如图,已知AB∥α,AD⊥α,BC⊥α,垂足为D、C,PA⊥AB,求证:CD⊥平面PAD.