题目内容
11.若抛物线x2=12y上一点(x0,y0)到焦点的距离是该点到x轴距离的4倍,则y0的值为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
分析 利用抛物线的定义与性质,转化列出方程求解即可.
解答 解:拋物线x2=24y上一点(x0,y0),到焦点的距离是该点到x轴距离的4倍,
可得y0+$\frac{p}{2}$=4y0,所以y0=$\frac{p}{6}$=$\frac{24}{2}$×$\frac{1}{6}$=2.
故选:C.
点评 本题考查抛物线的简单性质的应用,考查计算能力.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
15.三棱锥P-ABC的三条侧棱两两垂直,且PA=PB=PC=1,则其外接球上的点到平面ABC的距离的最大值为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{6}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
2.若如图框图所给的程序运行结果为S=41,图中的判断框①中是i>a,则实数a的取值范围是( )
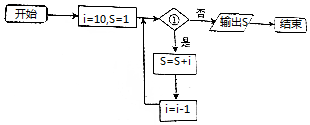

| A. | (5,6] | B. | [5,6) | C. | (6,7] | D. | [6,7) |
16.设向量$\overrightarrow{BA}$=(3,2),$\overrightarrow{BC}$=(3,-4),$\overrightarrow{AD}$=(0,2),则( )
| A. | $\overrightarrow{AB}∥\overrightarrow{BC}$ | B. | $\overrightarrow{AB}∥\overrightarrow{AD}$ | C. | $\overrightarrow{BC}∥\overrightarrow{AC}$ | D. | $\overrightarrow{AC}∥\overrightarrow{AD}$ |
3.从1,2,3,4,5这五个数字中选出三个不相同数组成一个三位数,则奇数位上必须是奇数的三位数个数为( )
| A. | 12 | B. | 18 | C. | 24 | D. | 30 |
1.P(x,y)是曲线$\left\{\begin{array}{l}x=-2+cosθ\\ y=sinθ\end{array}$(0≤θ<π,θ是参数)上的动点,则$\frac{y}{x}$的取值范围是( )
| A. | [-$\frac{\sqrt{3}}{3}$,0] | B. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] | C. | [0,$\frac{\sqrt{3}}{3}$] | D. | (-∞,$\frac{\sqrt{3}}{3}$] |
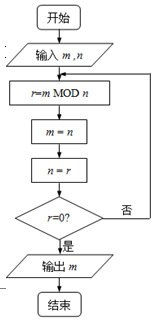 右边程序框图的算法思路源于数学名著《几何原本》中的“辗转
右边程序框图的算法思路源于数学名著《几何原本》中的“辗转