题目内容
3.从1,2,3,4,5这五个数字中选出三个不相同数组成一个三位数,则奇数位上必须是奇数的三位数个数为( )| A. | 12 | B. | 18 | C. | 24 | D. | 30 |
分析 根据题意,分2步进行分析:①、在1、3、5三个奇数中任选2个,安排在三位数的个位和百位,②、在剩余的3个数字中任选1个,将其安排在三位数的十位,分别求出每一步的情况数目,由分步计数原理计算可得答案.
解答 解:根据题意,要求奇数位上必须是奇数的三位数,则这个三位数的百位、个位为奇数,
分2步进行分析:
①、在1、3、5三个奇数中任选2个,安排在三位数的个位和百位,
有C32A22=6种情况,
②、在剩余的3个数字中任选1个,将其安排在三位数的十位,
有C31=3种情况,
则奇数位上必须是奇数的三位数有6×3=18个;
故选:B.
点评 本题考查排列、组合的实际应用,注意这个三位数的十位数字没有要求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.正四面体ABCD的棱长为4,E为棱AB的中点,过E作此正四面体的外接球的截面,则截面面积的最小值是( )
| A. | 4π | B. | 8π | C. | 12π | D. | 16π |
14.曲线$\left\{\begin{array}{l}{x=sinθ}\\{y=cos2θ}\end{array}\right.$(θ参数)在y轴上的截距为( )
| A. | 、$-\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
11.若抛物线x2=12y上一点(x0,y0)到焦点的距离是该点到x轴距离的4倍,则y0的值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
12.设$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$均为非零向量,若|($\overrightarrow{a}$+$\overrightarrow{b}$)•$\overrightarrow{c}$|=|($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{c}$|,则( )
| A. | $\overrightarrow{a}$∥$\overrightarrow{b}$ | B. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | C. | $\overrightarrow{a}$∥$\overrightarrow{c}$或$\overrightarrow{b}$∥$\overrightarrow{c}$ | D. | $\overrightarrow{a}$⊥$\overrightarrow{c}$或$\overrightarrow{b}$⊥$\overrightarrow{c}$ |
13. 如图,若程序框图运行后输出的结果是57,则判断框中应填入的条件是( )
如图,若程序框图运行后输出的结果是57,则判断框中应填入的条件是( )
 如图,若程序框图运行后输出的结果是57,则判断框中应填入的条件是( )
如图,若程序框图运行后输出的结果是57,则判断框中应填入的条件是( )| A. | A<4 | B. | A<5 | C. | A≤5 | D. | A≤6 |
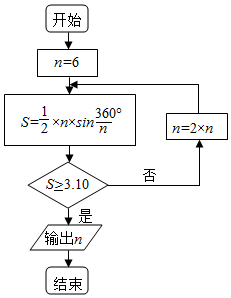 我国魏晋期间的伟大的数学家刘徽,是最早提出用逻辑推理的方式来论证数学命题的人,他创立了“割圆术”,得到了著名的“徽率”,即圆周率精确到小数点后两位的近似值3.14.如图就是利用“割圆术”的思想设计的一个程序框图,则输出的求n的值为(参考数据:sin15°=0.2588,sin7.5°=0.1305)( )
我国魏晋期间的伟大的数学家刘徽,是最早提出用逻辑推理的方式来论证数学命题的人,他创立了“割圆术”,得到了著名的“徽率”,即圆周率精确到小数点后两位的近似值3.14.如图就是利用“割圆术”的思想设计的一个程序框图,则输出的求n的值为(参考数据:sin15°=0.2588,sin7.5°=0.1305)( )