题目内容
已知数列{an}满足:a1=1,an+1=
(n∈N*).若bn+1=(n-λ)•(
+1)(n∈N*),b1=-λ,且数列{bn}是单调递增数列,求实数λ的取值范围.
| an |
| an+2 |
| 1 |
| an |
考点:数列递推式,数列的函数特性
专题:等差数列与等比数列
分析:由数列递推式得到数列{
+1}是首项为2,公比为2的等比数列,求出其通项公式后代入bn+1=(n-λ)•(
+1),由b2>b1求得实数λ的取值范围,验证满足bn+1=(n-λ)•2n为增函数得答案.
| 1 |
| an |
| 1 |
| an |
解答:
解:由an+1=
,得
=
+1,
则
+1=2(
+1),
由a1=1,得
+1=2,
∴数列{
+1}是首项为2,公比为2的等比数列,
∴
+1=2n.
由bn+1=(n-λ)•(
+1)=(n-λ)•2n,
∵b1=-λ,
b2=(1-λ)•2=2-2λ,
由b2>b1,得2-2λ>-λ,得λ<2,
此时bn+1=(n-λ)•2n为增函数,满足题意.
∴实数λ的取值范围是(-∞,2).
| an |
| an+2 |
| 1 |
| an+1 |
| 2 |
| an |
则
| 1 |
| an+1 |
| 1 |
| an |
由a1=1,得
| 1 |
| a1 |
∴数列{
| 1 |
| an |
∴
| 1 |
| an |
由bn+1=(n-λ)•(
| 1 |
| an |
∵b1=-λ,
b2=(1-λ)•2=2-2λ,
由b2>b1,得2-2λ>-λ,得λ<2,
此时bn+1=(n-λ)•2n为增函数,满足题意.
∴实数λ的取值范围是(-∞,2).
点评:本题考查了数列递推式,考查了数列的函数特性,关键是由数列递推式得到数列{
+1}是首项为2,公比为2的等比数列,是中档题.
| 1 |
| an |

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
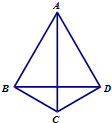 如图,将两个全等的30°的直角三角形ABC和直角三角形ADC拼在一起组成平面四边形ABCD,若
如图,将两个全等的30°的直角三角形ABC和直角三角形ADC拼在一起组成平面四边形ABCD,若| DB |
| DA |
| DC |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知f(x6)=log2x,则f(8)=( )
A、
| ||
| B、8 | ||
| C、18 | ||
D、
|
不等式(x-1)(x+2)≤0的解集是( )
| A、[1,2] |
| B、[-1,2] |
| C、[-2,1] |
| D、(-∞,-2]∪[1,+∞) |
若直线y=x+b与曲线x=3-
有公共点,则b的取值范围是( )
| 4y-y2 |
A、[-1-2
| ||||
B、[-3,-1+2
| ||||
C、[-1-2
| ||||
D、[-3,-1+
|