题目内容
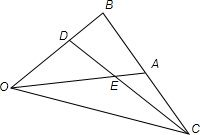如图，已知△OAB中，点C是点B关于A的对称点，点D是线段OB的一个靠近B的三等分点，DC和OA交于E，设 |
| AB |
|
| AO |
（1）用向量
| a |
| b |
| OC |
| CD |
（2）若
| OE |
| OA |
考点：向量的加法及其几何意义,向量的减法及其几何意义
专题：平面向量及应用
分析：（1）根据题意，利用向量的加法与减法的几何意义，得出
=
+
，
=
+
，即可用
、
表示；
（2）根据
与
共线，求出
与
的关系，从而得出
与
的关系．
| OC |
| OA |
| AC |
| CD |
| CB |
| BD |
| a |
| b |
（2）根据
| CD |
| CE |
| AE |
| AO |
| OE |
| OA |
解答：
解：（1）△OAB中，∵点C是点B关于A的对称点，
∴
=
=
，
∴
=-
，
∴
=
+
=-
+（-
）=-
-
；
又∵
=2
=2
，
点D是线段OB的一个靠近B的三等分点，
∴
=
；
又∵
=
+
=-
+
，
∴
=
+
=2
+
（-
+
）
=
+
；
（2）∵
=
+
，
设
=
+
=
+x
，
=y
，x、y∈R；
∴
+
=y
+xy
，
即
，
解得y=
，x=
；
∴
=
，
=
；
∴当
=λ
时，λ=
．
∴
| CA |
| AB |
| a |
∴
| AC |
| a |
∴
| OC |
| OA |
| AC |
| b |
| a |
| a |
| b |
又∵
| CB |
| AB |
| a |
点D是线段OB的一个靠近B的三等分点，
∴
| BD |
| 1 |
| 3 |
| BO |
又∵
| BO |
| BA |
| AO |
| a |
| b |
∴
| CD |
| CB |
| BD |
=2
| a |
| 1 |
| 3 |
| a |
| b |
=
| 5 |
| 3 |
| a |
| 1 |
| 3 |
| b |
（2）∵
| CD |
| 5 |
| 3 |
| a |
| 1 |
| 3 |
| b |
设
| CE |
| CA |
| AE |
| a |
| b |
| CD |
| CE |
∴
| 5 |
| 3 |
| a |
| 1 |
| 3 |
| b |
| a |
| b |
即
|
解得y=
| 5 |
| 3 |
| 1 |
| 5 |
∴
| AE |
| 1 |
| 5 |
| AO |
| OE |
| 4 |
| 5 |
| OA |
∴当
| OE |
| OA |
| 4 |
| 5 |
点评：本题考查了平面向量的加法与减法的几何意义以及向量共线的应用问题，是基础题目．
练习册系列答案
相关题目
函数f（x）=cos
(
sin
+cos
)的在下列哪个区间上单调递增（ ）
| x |
| 2 |
| 3 |
| x |
| 2 |
| x |
| 2 |
A、(
| ||||
B、(-
| ||||
C、(0，
| ||||
D、(-
|
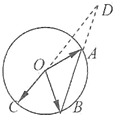如图所示，A，B，C是圆O上的三点，CO的延长线与线段BA的延长线交于圆外的点D，若| OC |
| OA |
| OB |
| A、（1，+∞） |
| B、（-∞，-1） |
| C、（0，1） |
| D、（-1，0） |
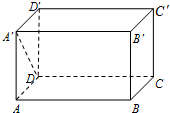如图，在长方体ABCD-A′B′C′D′中，AB=6，AA′=BC=4，则A′D与BC所成的角等于（ ）| A、30° | B、45° |
| C、60° | D、90° |