题目内容
已知α∈(0,π),求证:2sin2α≤
,试用综合法和分析法分别证明.
| sinα |
| 1-cosα |
考点:综合法与分析法(选修)
专题:证明题,分析法,综合法
分析:1.用综合法证明:将右边减去左边,通分,配方,由α∈(0,π),得cosα与sinα的范围,从而判断差式的符号,即可得证.
2.用分析法证明:利用二倍角公式,将“sin2α”改写为“2sinαcoaα”,从而原式等价于“4cosα≤
”,去分母,进一步转化为4cosα(1-cosα)≤1,即可化为完全平方式,得证.
2.用分析法证明:利用二倍角公式,将“sin2α”改写为“2sinαcoaα”,从而原式等价于“4cosα≤
| 1 |
| 1-cosα |
解答:
证明:(综合法)
-2sin2α
=sinα(
-4cosα)=
,
∵α∈(0,π),∴-1<cosα<1,0<sinα<1,
∴
≥0,即
-2sin2α≥0,
∴2sin2α≤
.
另证:(分析法)∵sin2α=2sinαcosα,
∴原不等式等价于4sinαcosα≤
.
又∵α∈(0,π),∴-1<cosα<1,0<sinα<1,
∴只需证4cosα≤
,化简,
得4cosα(1-cosα)≤1,即证(2cosα-1)2≥0,而此式显然成立,
故原不等式成立,得证.
| sinα |
| 1-cosα |
=sinα(
| 1 |
| 1-cosα |
| (1-2cosα)2sinα |
| 1-cosα |
∵α∈(0,π),∴-1<cosα<1,0<sinα<1,
∴
| (1-2cosα)2sinα |
| 1-cosα |
| sinα |
| 1-cosα |
∴2sin2α≤
| sinα |
| 1-cosα |
另证:(分析法)∵sin2α=2sinαcosα,
∴原不等式等价于4sinαcosα≤
| sinα |
| 1-cosα |
又∵α∈(0,π),∴-1<cosα<1,0<sinα<1,
∴只需证4cosα≤
| 1 |
| 1-cosα |
得4cosα(1-cosα)≤1,即证(2cosα-1)2≥0,而此式显然成立,
故原不等式成立,得证.
点评:本题考查了利用综合法及分析法证明三角不等式,关键是掌握综合法与分析法的原理、步骤及格式.

练习册系列答案
相关题目
如图是正方体的平面展开图,在这个正方体中,正确的命题是( )
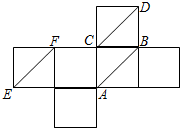

| A、BD与CF成60°角 |
| B、BD与EF成60°角 |
| C、AB与CD成60°角 |
| D、AB与EF成60°角 |