题目内容
在△ABC中,角A,B,C对应的边分别为a,b,c,且a=3,b=3,cosB=
.
(Ⅰ)求边c的长度;
(Ⅱ)求cos(B-C)的值.
| 1 |
| 3 |
(Ⅰ)求边c的长度;
(Ⅱ)求cos(B-C)的值.
考点:余弦定理,正弦定理
专题:解三角形
分析:(Ⅰ)利用余弦定理列出关系式,把a,b,cosB的值代入求出边c的长即可;
(Ⅱ)由cosB的值求出sinB的值,再由b与c的值,利用正弦定理求出sinC的值,确定出cosC的值,原式利用两角和与差的余弦函数公式化简,将各自的值代入计算即可求出值.
(Ⅱ)由cosB的值求出sinB的值,再由b与c的值,利用正弦定理求出sinC的值,确定出cosC的值,原式利用两角和与差的余弦函数公式化简,将各自的值代入计算即可求出值.
解答:
解:(Ⅰ)由余弦定理,得b2=a2+c2-2accosB,
∵a=b=3,cosB=
,
∴9=9+c2-2c,
解得:c=2(c=0舍去);
(Ⅱ)在△ABC中,sinB=
=
,
由正弦定理
=
,得sinC=
=
,
∵a=b>c,∴C为锐角,
∴cosC=
=
,
则cos(B-C)=cosBcosC+sinBsinC=
×
+
×
=
.
∵a=b=3,cosB=
| 1 |
| 3 |
∴9=9+c2-2c,
解得:c=2(c=0舍去);
(Ⅱ)在△ABC中,sinB=
| 1-cos2B |
2
| ||
| 3 |
由正弦定理
| b |
| sinB |
| c |
| sinC |
| csinB |
| b |
4
| ||
| 9 |
∵a=b>c,∴C为锐角,
∴cosC=
| 1-sin2C |
| 7 |
| 9 |
则cos(B-C)=cosBcosC+sinBsinC=
| 1 |
| 3 |
| 7 |
| 9 |
2
| ||
| 3 |
4
| ||
| 9 |
| 23 |
| 27 |
点评:此题考查了正弦、余弦定理,同角三角函数间的基本关系,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
已知函数f(x)=x+
+m(p≠0)是奇函数,
(1)求m的值;
(2)若p=-1,用定义证明函数f(x)=x-
在区间(0,+∞)上的单调性.
(3)若p<0,当x∈[1,3]时,求f(x)的最值.
| p |
| x |
(1)求m的值;
(2)若p=-1,用定义证明函数f(x)=x-
| 1 |
| x |
(3)若p<0,当x∈[1,3]时,求f(x)的最值.
若△ABC的三个内角A、B、C成等差数列,则cos(A+C)=( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
若集合A={x|
≤0},B={x|x≥-2}且A⊆B.则实数a的取值范围是( )
| x-a |
| x-2 |
| A、(-∞,-2] |
| B、[-2,2] |
| C、[-2,+∞) |
| D、[2,+∞) |
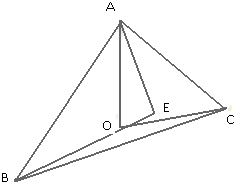 如图,O为△ABC的外心,E为三角形内一点,满足
如图,O为△ABC的外心,E为三角形内一点,满足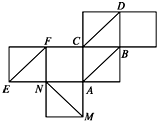 如图为棱长是1的正方体的表面展开图,在原正方体中,给出下列三个命题:
如图为棱长是1的正方体的表面展开图,在原正方体中,给出下列三个命题: