题目内容

若点P（x，y）满足
y≤1
x-y-1≤0
x+y-1≥0
则点P（x，y）到坐标原点O的距离的最大值为
 
．
考点：简单线性规划
专题：计算题,作图题,不等式的解法及应用
分析：由题意作出其平面区域，由图可知，P（x，y）与B重合时，取得最大值．
解答： 解：由题意作出其平面区域，

则P（x，y）与B重合时，取得最大值，
则P（2，1），
则点P（x，y）到坐标原点O的距离的最大值为
22+1
=
5
，
故答案为：
5
．
点评：本题考查了简单线性规划，作图要细致认真，属于中档题．
练习册系列答案
相关题目
在数列{an}，{bn}中，a1=2，b1=4且an，bn，an+1成等差数列，bn，an+1，bn+1成等比数列（n∈N*）
（1）求a2，a3，a4及b2，b3，b4；由此归纳出{an}，{bn}的通项公式，并证明你的结论．
（2）若cn=log2（
bn
an
），Sn=c1+c2+…+cn，试问是否存在正整数m，使Sm≥5，若存在，求最小的正整数m．
已知函数f（x）=
sin2x-
3
cos2x+
3
sinx
．
（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）求使得不等式f（x）≤-2成立的x的取值集合．
已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左右分别为F1，F2，点P在双曲线的右支上，且|PF1|=2015|PF2|，则此双曲线的离心率e的最大值为
 
．
已知点A（-3，5），B（2，15），P是直线x-y+5=0上的动点，则|PA|+|PB|的最小值为
 
．
在△ABC中，a=b+2，b=c+2，且最大角是120°，求△ABC的面积．
函数f（x）=log2（-x2+ax+3）在（2，4）是单调递减的，则a的范围是（　　）
A、（
13
4
，4]
B、[
13
4
，4]
C、[8，+∞）
D、（-∞，4]
已知实数R为全集，集合A={x|y=log2（x-1）}，B={y|y=
4x-x2
}，则（∁RA）∩B等于（　　）
A、（-∞，1]
B、（0，1）
C、[0，1]
D、（1，2]
函数f（x）（x∈R）的图象如图所示，则函数g（x）=f（log 
1
4
x）的单调减区间是（　　）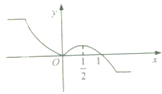
A、[0，
1
2
]
B、（-∞，0）∪[
1
2
，+∞）
C、[
1
2
，1]
D、[
1
2
，
3
2
]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网