Question

函数f（x）（x∈R）的图象如图所示，则函数g（x）=f（log 

1

4

x）的单调减区间是（　　）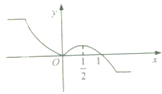

• A、[0，

  1

  2

  ]
• B、（-∞，0）∪[

  1

  2

  ，+∞）
• C、[

  1

  2

  ，1]
• D、[

  1

  2

  ，

  3

  2

  ]

Answer 1

考点：复合函数的单调性

专题：函数的性质及应用

分析：直接由图象得到函数f（x）增区间，再由复合函数的单调性得到使函数g（x）=f（log 

1

4

x）单调递减的x的范围．

解答： 解：由图可知，函数f（x）的得到增区间为[0，

1

2

]，
而内层函数log 

1

4

x为减函数，
则内函数log 

1

4

x的减区间即为复合函数g（x）=f（log 

1

4

x）的单调减区间．
由log 

1

4

x=0，得x=1，
由log 

1

4

x=

1

2

，得x=

1

2

．
∴函数g（x）=f（log 

1

4

x）的单调减区间是[

1

2

，1]．
故选：C．

点评：本题考查了复合函数的单调性，考查了对数的运算性质，是中档题．