题目内容

求下列函数的导数：
（1）y=2x
（2）y=lnx
（3）y=x3+cosx．
考点：导数的运算
专题：导数的概念及应用
分析：根据导数公式进行计算即可得到结论．
解答： 解：（1）y′=（2x ）′=2xln2；
（2）y′=（lnx）′=
1
x
（3）y′=（x3）′+（cosx）′=3x2-sinx，
点评：本题考查了导数的运算，牢记求导公式是解本题的关键．
练习册系列答案
相关题目
设a，b∈R+，a+b=1，则
a2+1
+
b2+4
的最小值为（　　）
A、2+
2
B、2
2
C、3
D、
10
（1）已知x1＞0，x2＞0且x1+x2=1，求x1log2x1+x2log2x2的最小值；
（2）已知xi＞0（i=1，2，3，4）且x1+x2+x3+x4=1，求证：x1log2x1+x2log2x2+x3log2x3+x4log2x4≥-2；
（3）已知xi＞0（i=1，2，3，4，5，6，7，8）且x1+x2+x3+…+x8=1，类比（2）给出一个你认为正确的结论，并证明你的结论．
已知a是实数，函数f（x）=x3-ax2-4x+4a．
（1）若f′（-1）=0，求实数a的值；
（2）若函数f（x）在（-∞，-2）和（2，+∞）上都是单调递增的，求实数a的取值范围．
已知an=
3n-1，(n为偶数)
2n，(n为奇数)
，Sn是其前n项的和，求S9和S2n．
圆具有性质：设M、N是圆C：x2+y2=r2关于原点对称的两个点，P是圆C上任意一点，直线PM，PN的斜率kPM，kPN存在，则kPM•kPN=-1，类比上述性质，在椭圆C：
x2
a2
+
y2
b2
=1中，写出相类似的性质，并给出证明．
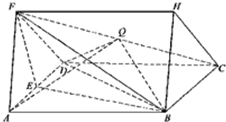如图，三棱柱ADF-BCH中，侧面ABCD是菱形，FA=FD，∠BAD=60°，E是AD的中点，点Q在线段FC上．
（Ⅰ）求证：AD⊥平面EFB；
（Ⅱ）若Q是FC的中点，求证：FA∥平面BDQ
（Ⅲ）若VF-BCDE=2VQ-ABCD，试求
CF
CQ
的值．
已知向量
m
=（2sinωx，cosωx），
n
=（-
3
sinωx，2sinωx）（ω＞0）函数f（x）=
m
•
n
+
3
，直线x=x1，x=x2是函数y=f（x）的图象的任意两条对称轴，且|x1-x2|的最小值为
π
2
．
（1）求ω的值和函数f（x）的单调增区间；
（2）已知x∈[-
π
3
，θ]，f（x）∈[-
3
，2]，求θ的取值范围．
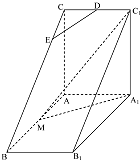如图，直三棱柱ABC=A1B1C1中，AC⊥AB，AB=2AA1，M是AB的中点，△A1MC1是等腰三角形，D为CC1的中点，E为BC上一点且
CE
EB
=
1
3
．
（Ⅰ）证明：DE∥平面A1MC1；
（Ⅱ）若AB=2，求三棱锥E-A1MC1的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网