题目内容
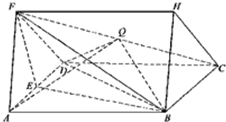如图，三棱柱ADF-BCH中，侧面ABCD是菱形，FA=FD，∠BAD=60°，E是AD的中点，点Q在线段FC上．（Ⅰ）求证：AD⊥平面EFB；
（Ⅱ）若Q是FC的中点，求证：FA∥平面BDQ
（Ⅲ）若VF-BCDE=2VQ-ABCD，试求
| CF |
| CQ |
考点：直线与平面垂直的判定,棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题：综合题,空间位置关系与距离
分析：（Ⅰ）利用线面垂直的判定证明，关键是证明AD⊥FE，AD⊥BE；
（Ⅱ）连接AC交BD于点O，连结OQ，利用三角形的中位线定理证明OQ∥FA，即可证明FA∥平面BDQ
（Ⅲ）利用体积关系可得高的关系，即可求
的值．
（Ⅱ）连接AC交BD于点O，连结OQ，利用三角形的中位线定理证明OQ∥FA，即可证明FA∥平面BDQ
（Ⅲ）利用体积关系可得高的关系，即可求
| CF |
| CQ |
解答：
（Ⅰ）证明：因为E是AD的中点，FA=FD，所以AD⊥FE
因为侧面ABCD是菱形，∠BAD=60°，所以AB=BD，
又因为E是AD的中点，所以AD⊥BE，
因为FE∩BE=E，所以AD⊥平面EFB…..（4分）
（Ⅱ）证明：连接AC交BD于点O，连结OQ．
因为O是AC中点，Q是FC的中点，
所以OQ为△FAC的中位线，
所以OQ∥FA，
因为FA?平面BDQ，OQ?平面BDQ，
所以FA∥平面BDQ…．（8分）
（Ⅲ）解：设四棱锥F-BCDE，Q-ABCD的高分别为h1，h2，
所以VF-BCDE=
SBCDEh1，VQ-ABCD=
SABCDh2
因为VF-BCDE=2VQ-ABCD，且底面积SBCDE=
SABCD
所以
=
，
因为
=
，
所以
=
…（12分）
因为侧面ABCD是菱形，∠BAD=60°，所以AB=BD，
又因为E是AD的中点，所以AD⊥BE，
因为FE∩BE=E，所以AD⊥平面EFB…..（4分）
（Ⅱ）证明：连接AC交BD于点O，连结OQ．
因为O是AC中点，Q是FC的中点，
所以OQ为△FAC的中位线，
所以OQ∥FA，
因为FA?平面BDQ，OQ?平面BDQ，
所以FA∥平面BDQ…．（8分）
（Ⅲ）解：设四棱锥F-BCDE，Q-ABCD的高分别为h1，h2，
所以VF-BCDE=
| 1 |
| 3 |
| 1 |
| 3 |
因为VF-BCDE=2VQ-ABCD，且底面积SBCDE=
| 3 |
| 4 |
所以
| h1 |
| h2 |
| 8 |
| 3 |
因为
| h1 |
| h2 |
| CF |
| CQ |
所以
| CF |
| CQ |
| 8 |
| 3 |
点评：本题考查线面垂直，考查线面平行，考查体积的计算，解题的关键是掌握线面垂直、线面平行的判定，属于中档题．
练习册系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目