题目内容
函数f(x)=mx3+(m+1)x2+x+2,若f′(1)=18,则m=( )
| A、4 | B、3 | C、5 | D、6 |
考点:导数的运算
专题:计算题,导数的概念及应用
分析:先求出f'(x)=3mx3+2(m+1)x+1,代入x=1,建立方程求解即可.
解答:
解:∵f(x)=mx3+(m+1)x2+x+2,
∴f'(x)=3mx3+2(m+1)x+1,
∴f'(1)=3m+2(m+1)+1
=5m+3=18
∴m=3.
故选:B.
∴f'(x)=3mx3+2(m+1)x+1,
∴f'(1)=3m+2(m+1)+1
=5m+3=18
∴m=3.
故选:B.
点评:本题考查基本函数的导数公式和导数加法法则的应用,属于基础题.

练习册系列答案
相关题目
如果命题p:|x-1|+|y-2|=0,命题q:(x-1)(y-2)=0,那么命题p是命题q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
为了调查城市PM2.5的情况,按地域把48个城市分成大型、中型、小型三组,对应的城市数分别为8,16,24.若用分层抽样的方法抽取12个城市,则中型组中应抽取的城市数为( )
| A、3 | B、4 | C、5 | D、6 |
设向量
=(2,1),
=(-1,y),若
∥
,则y的值为( )
| a |
| b |
| a |
| b |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
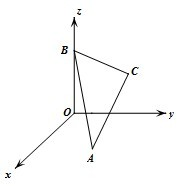 如图,空间直角坐标系Oxyz中,正三角形ABC的顶点A,B分别在xOy平面和z轴上移动.若AB=2,则点C到原点O的最远距离为( )
如图,空间直角坐标系Oxyz中,正三角形ABC的顶点A,B分别在xOy平面和z轴上移动.若AB=2,则点C到原点O的最远距离为( )A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
已知函数f(x)=x-[x],x∈R,其中[x]表示不超过x的最大整数,如[-
]=-2,[-3]=-3,[
]=2,则f(x)的值域是( )
| 3 |
| 2 |
| 5 |
| 2 |
| A、(0,1) |
| B、(0,1] |
| C、[0,1) |
| D、[0,1] |