题目内容
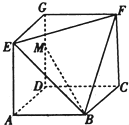 已知几何体EFG-ABCD如图所示,其中四边形ABCD,CDGF,ADGE均为正方形,且边长为1,点M在边DG上.
已知几何体EFG-ABCD如图所示,其中四边形ABCD,CDGF,ADGE均为正方形,且边长为1,点M在边DG上.(1)求证:BM⊥EF;
(2)是否存在点M,使得直线MB与平面BEF所成的角为45°.若存在,试求点M的位置.
考点:直线与平面所成的角,空间中直线与直线之间的位置关系
专题:计算题,作图题,证明题,空间位置关系与距离
分析:如图,连结AC、BD,交于点O,作OH∥AE,交EF于点H,连结BH,
(1)可证明EF∥AC;再证明AC⊥平面BDG,从而可证明EF⊥平面BDG,从而证明BM⊥EF;
(2)易知∠HBO是平面BEF与平面ABCD所成的角,从而求出tan∠HBO=
=
>1,说明存在,再由三角恒等变换求MD的长度即可.
(1)可证明EF∥AC;再证明AC⊥平面BDG,从而可证明EF⊥平面BDG,从而证明BM⊥EF;
(2)易知∠HBO是平面BEF与平面ABCD所成的角,从而求出tan∠HBO=
| HO |
| OB |
| 2 |
解答:
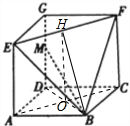 解:如图,连结AC、BD,交于点O,作OH∥AE,交EF于点H,连结BH,
解:如图,连结AC、BD,交于点O,作OH∥AE,交EF于点H,连结BH,
(1)证明:∵四边形ABCD,CDGF,ADGE均为正方形,
∴AE=CF,AE∥CF,
∴AEFC是平行四边形,
∴EF∥AC;
又∵AC⊥BD,
DG⊥AC,
∴AC⊥平面BDG,
∴EF⊥平面BDG,
又∵BM?平面BDG,
∴BM⊥EF;
(2)易知∠HBO是平面BEF与平面ABCD所成的角,
在Rt△BOH中,
OH=1,BO=
,
则tan∠HBO=
=
>1,
∴存在点M,使得直线MB与平面BEF所成的角为45°,
∠MBH为直线MB与平面BEF所成的角,
若∠MBH=45°,
则tan∠MBD=tan(∠HBO-45°)
=
=3-2
,
故
=3-2
,
则MD=3
-4.
 解:如图,连结AC、BD,交于点O,作OH∥AE,交EF于点H,连结BH,
解:如图,连结AC、BD,交于点O,作OH∥AE,交EF于点H,连结BH,(1)证明:∵四边形ABCD,CDGF,ADGE均为正方形,
∴AE=CF,AE∥CF,
∴AEFC是平行四边形,
∴EF∥AC;
又∵AC⊥BD,
DG⊥AC,
∴AC⊥平面BDG,
∴EF⊥平面BDG,
又∵BM?平面BDG,
∴BM⊥EF;
(2)易知∠HBO是平面BEF与平面ABCD所成的角,
在Rt△BOH中,
OH=1,BO=
| ||
| 2 |
则tan∠HBO=
| HO |
| OB |
| 2 |
∴存在点M,使得直线MB与平面BEF所成的角为45°,
∠MBH为直线MB与平面BEF所成的角,
若∠MBH=45°,
则tan∠MBD=tan(∠HBO-45°)
=
| ||
|
| 2 |
故
| MD |
| BD |
| 2 |
则MD=3
| 2 |
点评:本题考查了学生的空间想象力与作图能力,同时考查了三角恒等变换及三角函数的定义,属于中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
过椭圆
+
=1(a>0)的焦点F作一直线交椭圆于P、Q两点,若线段PF、QF的长分别是p、q,则
+
=( )
| x2 |
| 4a2 |
| y2 |
| a2 |
| 1 |
| p |
| 1 |
| q |
A、
| ||
B、
| ||
| C、4a | ||
| D、2a |
已知动点P(x,y)满足
,点Q(1,-1),O为坐标原点,λ|
|=
•
,则实数λ的取值范围是( )
|
| OP |
| OP |
| OQ |
A、[-
| ||||||||
B、[
| ||||||||
C、[-
| ||||||||
D、[-
|