题目内容
设0≤x≤1,求函数f(x)=4x+(1-2a)2x+1+a2的最小值m.
考点:函数的最值及其几何意义
专题:计算题,函数的性质及应用
分析:利用配方法化简f(x)=4x+(1-2a)2x+1+a2=(2x)2+2(1-2a)2x+a2=(2x+1-2a)2-3a2+4a-1,从而讨论求函数的求最小值.
解答:
解:f(x)=4x+(1-2a)2x+1+a2
=(2x)2+2(1-2a)2x+a2
=(2x+1-2a)2-3a2+4a-1,
①当1-2a≤-2,即a≥
时,
f(x)在x=1处有最小值,
m=f(1)=4+4(1-2a)+a2=a2-8a+8;
②当-2<1-2a<-1,即1<a<
时,
m=fmin(x)=-3a2+4a-1,
③当1-2a≥-1,即a≤1时,
m=f(0)=a2-4a+3.
综上所述,m=
.
=(2x)2+2(1-2a)2x+a2
=(2x+1-2a)2-3a2+4a-1,
①当1-2a≤-2,即a≥
| 3 |
| 2 |
f(x)在x=1处有最小值,
m=f(1)=4+4(1-2a)+a2=a2-8a+8;
②当-2<1-2a<-1,即1<a<
| 3 |
| 2 |
m=fmin(x)=-3a2+4a-1,
③当1-2a≥-1,即a≤1时,
m=f(0)=a2-4a+3.
综上所述,m=
|
点评:本题考查了配方法求函数的最值及分类讨论的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=
+
( )
| 3-x2 |
| 9 |
| |x|+1 |
| A、只是偶函数 |
| B、只是奇函数 |
| C、既是偶函数,又是奇函数 |
| D、是非奇非偶函数 |
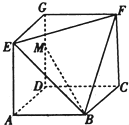 已知几何体EFG-ABCD如图所示,其中四边形ABCD,CDGF,ADGE均为正方形,且边长为1,点M在边DG上.
已知几何体EFG-ABCD如图所示,其中四边形ABCD,CDGF,ADGE均为正方形,且边长为1,点M在边DG上.