题目内容
已知动点P(x,y)满足
,点Q(1,-1),O为坐标原点,λ|
|=
•
,则实数λ的取值范围是( )
|
| OP |
| OP |
| OQ |
A、[-
| ||||||||
B、[
| ||||||||
C、[-
| ||||||||
D、[-
|
考点:简单线性规划
专题:不等式的解法及应用
分析:根据向量的数量积公式将条件进行化简,利用数形结合即可得到结论.
解答:
解:∵λ|
|=
•
=|
|•|
|cos<
,
>,
∴λ=|
|cos<
,
>=
cos<
,
>,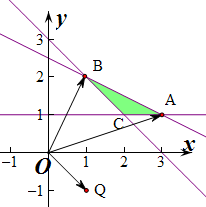
作出不等式组对应的平面区域如图,
则OQ,OA的夹角最小,OQ,OB的夹角最大,
由
,解得
,即A(3,1),
由
,解得
,即B(1,2),
则
=(3,1),
=(1,2),
则cos<
,
>=
=
=
=
,
cos<
,
>=
=
=-
,
∴-
≤cos<
,
>≤
,
即-
≤
cos<
,
>≤
,
即-
≤λ≤
,
故选:D
| OP |
| OP |
| OQ |
| OP |
| OQ |
| OP |
| OQ |
∴λ=|
| OQ |
| OP |
| OQ |
| 2 |
| OP |
| OQ |

作出不等式组对应的平面区域如图,
则OQ,OA的夹角最小,OQ,OB的夹角最大,
由
|
|
由
|
|
则
| OA |
| OB |
则cos<
| OA |
| OQ |
| ||||
|
|
| 3-1 | ||||
|
| 2 | ||
2
|
| ||
| 5 |
cos<
| OB |
| OQ |
| ||||
|
|
| 1-2 | ||||
|
| ||
| 10 |
∴-
| ||
| 10 |
| OP |
| OQ |
| ||
| 5 |
即-
| ||
| 5 |
| 2 |
| OP |
| OQ |
| ||
| 5 |
即-
| ||
| 5 |
| ||
| 5 |
故选:D
点评:本题主要考查线性规划的应用,结合向量数量积的应用,利用数形结合是解决本题的关键.综合性较强,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
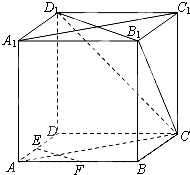 如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.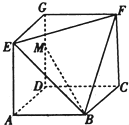 已知几何体EFG-ABCD如图所示,其中四边形ABCD,CDGF,ADGE均为正方形,且边长为1,点M在边DG上.
已知几何体EFG-ABCD如图所示,其中四边形ABCD,CDGF,ADGE均为正方形,且边长为1,点M在边DG上.