题目内容
已知数列{an}满足:a1=0,an+1=an+2
+1,n∈N*.
(Ⅰ)证明:数列{
}是等差数列;
(Ⅱ)设an=(
)2-1,求正项数列{bn}的前n和Sn.
| an+1 |
(Ⅰ)证明:数列{
| an+1 |
(Ⅱ)设an=(
| bn |
| 3n |
考点:数列的求和,等差数列的通项公式
专题:点列、递归数列与数学归纳法
分析:本题(Ⅰ)利用递推公式得到数列{
}的第n+1与第n项的关系,根据等差数列定义得到数列{
}是等差数列;(Ⅱ)利用已知数列{
}的通项公式,求出bn的通项公式,用错位相减法,求出正项数列{bn}的前n和Sn,得到本题结论.
| an+1 |
| an+1 |
| an+1 |
解答:
解:(Ⅰ)∵an+1=an+2
+1,n∈N*,
∴an+1+1=(
+1)2.
则:
-
=1,
所以数列{an+1}是以
=1为首项,公差为1的等差数列.
(Ⅱ)由(Ⅰ)知
=n,
∴an=n2-1.
∵an=(
)2-1,
∴bn=n•3n.
∴Sn=1•3+2•32+3•33+…+n•3n,…①
3Sn=1•32+2•33+3•34+…+n•3n+1,…②
由①-②得:Sn=
+
.
| an+1 |
∴an+1+1=(
| an+1 |
则:
| an+1+1 |
| an+1 |
所以数列{an+1}是以
| a1+1 |
(Ⅱ)由(Ⅰ)知
| an+1 |
∴an=n2-1.
∵an=(
| bn |
| 3n |
∴bn=n•3n.
∴Sn=1•3+2•32+3•33+…+n•3n,…①
3Sn=1•32+2•33+3•34+…+n•3n+1,…②
由①-②得:Sn=
| 3 |
| 4 |
| (2n-1)3n+1 |
| 4 |
点评:本题考查了数列的递推公式、错位相减法求和,本题难度不大,属于基础题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
若PO⊥平面ABC,O为垂足,∠ABC=90°,∠BAC=30°,BC=5,PA=PB=PC=10,则PO的长等于( )
| A、5 | ||
B、5
| ||
| C、10 | ||
D、10
|
若一个三角形,采用斜二测画法作出其直观图,则其直观图的面是原三角形面积的( )
A、
| ||||
| B、2倍 | ||||
C、
| ||||
D、
|

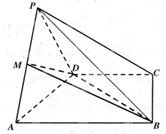 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.