题目内容
已知直线l:y=3x+3.
(1)求点P(5,3)关于直线l的对称点P′的坐标;
(2)求直线l1:x-y-2=0关于直线l的对称直线l2的方程;
(3)已知点M(2,6),试在直线l上求一点N使得|NP|+|NM|的值最小.
(1)求点P(5,3)关于直线l的对称点P′的坐标;
(2)求直线l1:x-y-2=0关于直线l的对称直线l2的方程;
(3)已知点M(2,6),试在直线l上求一点N使得|NP|+|NM|的值最小.
考点:与直线关于点、直线对称的直线方程
专题:计算题,直线与圆
分析:(1)设点P的对称点为P'(a,b),由中点坐标公式和两直线垂直的条件列方程,解出即可;
(2)首先求出两直线的交点,再由点关于直线对称的求法求出对称点,再由直线方程的形式,即可得到;
(3)可由(1)的结论,连接P'M,交直线l于N,连接NP,再由三点共线的知识,即可求出N.
(2)首先求出两直线的交点,再由点关于直线对称的求法求出对称点,再由直线方程的形式,即可得到;
(3)可由(1)的结论,连接P'M,交直线l于N,连接NP,再由三点共线的知识,即可求出N.
解答:
解:(1)设点P的对称点为P'(a,b),
则
,解得:
,
即点P'的坐标为(-4,6);
(2)解方程组
得
,
即两直线l与l的交点坐标为(-
,-
)
因为直线l与l2关于直线l对称,所以直线l2必过点(-
,-
),
又由(1)可知,点P(5,3)恰好在直线l上,且其关于直线l的对称点为P'(-4,6),
所以直线l2必过点P'(-4,6),这样由两点式可得:
=
,
即7x+y+22=0;
(3)由(1)得P'(-4,6),连接P'M,交直线l于N,连接NP,
则|NP|+|NM|=|NP'|+|NM|=|P'M|最小,
设出N(x,3x+3),则由P',M,N共线,可得,
=
,解得,x=1,
则可得N(1,6).
则
|
|
即点P'的坐标为(-4,6);
(2)解方程组
|
|
即两直线l与l的交点坐标为(-
| 5 |
| 2 |
| 9 |
| 2 |
因为直线l与l2关于直线l对称,所以直线l2必过点(-
| 5 |
| 2 |
| 9 |
| 2 |
又由(1)可知,点P(5,3)恰好在直线l上,且其关于直线l的对称点为P'(-4,6),
所以直线l2必过点P'(-4,6),这样由两点式可得:
y+
| ||
6+
|
x+
| ||
-4+
|
即7x+y+22=0;
(3)由(1)得P'(-4,6),连接P'M,交直线l于N,连接NP,
则|NP|+|NM|=|NP'|+|NM|=|P'M|最小,
设出N(x,3x+3),则由P',M,N共线,可得,
| 6-6 |
| -4-2 |
| 3x+3-6 |
| x-2 |
则可得N(1,6).
点评:本题考查点关于直线对称、直线关于直线对称,以及运用:求最值,考查直线方程的知识,考查运算能力,属于中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
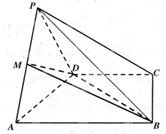 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 已知算法:
已知算法: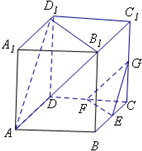 如图,在正方体ABCD=A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.
如图,在正方体ABCD=A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.