题目内容
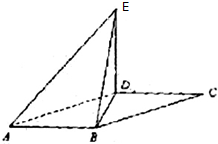 如图,平行四边形ABCD中,∠ABD=90°,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD.
如图,平行四边形ABCD中,∠ABD=90°,AB=2,AD=4,将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD.(1)求证:AB⊥DE;
(Ⅱ)求三棱锥E-ABD的侧面积.
考点:直线与平面垂直的性质,棱柱、棱锥、棱台的侧面积和表面积
专题:空间位置关系与距离
分析:(Ⅰ)DE⊥BD,根据面面垂直的性质定理,容易说明DE⊥平面ABD,又AB?平面ABD,所以AB⊥DE;
(Ⅱ)容易判断出△ABE,△ADE,△BDE都是直角三角形,所以只需求出一些直角边,即可求出这三个三角形的面积,也就求出了三棱锥E-ABD的侧面积.
(Ⅱ)容易判断出△ABE,△ADE,△BDE都是直角三角形,所以只需求出一些直角边,即可求出这三个三角形的面积,也就求出了三棱锥E-ABD的侧面积.
解答:
解:(Ⅰ)∵∠ABD=90°,∴AB⊥BD,AB∥CD,∴CD⊥BD,∴DE⊥BD;
∵平面EDB⊥平面ABD,平面EDB∩平面ABD=BD,DE?平面EDB,DE⊥BD;
∴DE⊥平面ABD,AB?平面ABD;
∴DE⊥AB,即AB⊥DE;
(Ⅱ)AB⊥DE,AB⊥BD,DE∩BD=D;
∴AB⊥平面EDB,BE?平面EDB,∴AB⊥BE,∴△ABE为Rt△;
ED⊥平面ABD,AD?平面ABD,∴ED⊥AD,∴△ADE为Rt△;
前面知道ED⊥BD,∴△BDE为Rt△;
在RtABD中,BD=
=2
,∴S△BDE=
BD•DE=2
;
S△ADE=
AD•DE=4;
在Rt△BDE中,BE=
=4,∴S△ABE=
AB•BE=4;
∴三棱锥E-ABD的侧面积为:8+2
.
∵平面EDB⊥平面ABD,平面EDB∩平面ABD=BD,DE?平面EDB,DE⊥BD;
∴DE⊥平面ABD,AB?平面ABD;
∴DE⊥AB,即AB⊥DE;
(Ⅱ)AB⊥DE,AB⊥BD,DE∩BD=D;
∴AB⊥平面EDB,BE?平面EDB,∴AB⊥BE,∴△ABE为Rt△;
ED⊥平面ABD,AD?平面ABD,∴ED⊥AD,∴△ADE为Rt△;
前面知道ED⊥BD,∴△BDE为Rt△;
在RtABD中,BD=
| 16-4 |
| 3 |
| 1 |
| 2 |
| 3 |
S△ADE=
| 1 |
| 2 |
在Rt△BDE中,BE=
| 12+4 |
| 1 |
| 2 |
∴三棱锥E-ABD的侧面积为:8+2
| 3 |
点评:考查面面垂直的性质定理,直角三角形边的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<
已知函数y=Asin(ωx+φ)+B的一部分图象如图所示,如果A>0,ω>0,|φ|<