题目内容
若ab＜0，求
+
的取值范围．
| b |
| a |
| a |
| b |
考点：基本不等式
专题：不等式的解法及应用
分析：本题可以先将负值转化成正值，再利用基本不等式求出取值范围．
解答：
解：∵ab＜0，
∴
＜0．
∴-
＞0，-
＞0．
∴(-
)+(-
)≥2
=2，
即-（
+
）≥2，
∴
+
≤-2．
∴
+
的取值范围是（-∞，-2]．
∴
| a |
| b |
∴-
| a |
| b |
| b |
| a |
∴(-
| a |
| b |
| b |
| a |
(-
|
即-（
| a |
| b |
| b |
| a |
∴
| a |
| b |
| b |
| a |
∴
| b |
| a |
| a |
| b |
点评：本题考查的基本不等式和化归转化的数学思想，本题有一定的技巧性，属于基础题．
练习册系列答案
相关题目
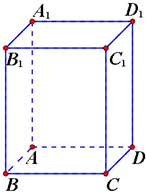长方体ABCD-A1B1C1D1中，宽、长、高分别为3、4、5，现有一个小虫从A出发沿长方体表面爬行到C1来获取食物，求其路程的最小值．
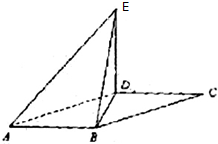如图，平行四边形ABCD中，∠ABD=90°，AB=2，AD=4，将△CBD沿BD折起到△EBD的位置，使平面EDB⊥平面ABD．
