题目内容
若a是1+2b与1-2b的等比中项,则
的最大值为 .
| 2ab |
| |a|+2|b| |
考点:等比数列的性质
专题:综合题,等差数列与等比数列
分析:由a是1+2b与1-2b的等比中项得到4|ab|≤1,再由基本不等式法求得
的最大值.
| 2ab |
| |a|+2|b| |
解答:
解:a是1+2b与1-2b的等比中项,则a2=1-4b2⇒a2+4b2=1≥4|ab|.
∴|ab|≤
.
∵a2+4b2=(|a|+2|b|)2-4|ab|=1.
∴
≤
=
∵|ab|≤
∴
≥4,
∴
的最大值为
=
.
故答案为:
.
∴|ab|≤
| 1 |
| 4 |
∵a2+4b2=(|a|+2|b|)2-4|ab|=1.
∴
| 2ab |
| |a|+2|b| |
| 2|ab| | ||
|
|
∵|ab|≤
| 1 |
| 4 |
∴
| 1 |
| |ab| |
∴
| 2ab |
| |a|+2|b| |
|
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:本题考查等比中项以及不等式法求最值问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
圆x2+y2+ax+2=0与直线l相切于点A(-3,1)则直线l的方程为( )
| A、x+y+2=0 |
| B、x-2y-2=0 |
| C、x-y+4=0 |
| D、2x-y-5=0 |
m=2是复数(m-2)+(m2-3m+2)i(m∈R)是纯虚数的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分且必要条件 |
| D、既不充分也不必要条件 |
直线x-
y=0截圆x2+y2-4x=0所得劣弧所对的圆心角是( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
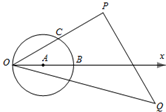 如图,在极坐标系中,设极径为ρ(ρ>0),极角为θ(0≤θ<2π),⊙A的极坐标方程为ρ=2cosθ,点C在极轴的上方,∠AOC=
如图,在极坐标系中,设极径为ρ(ρ>0),极角为θ(0≤θ<2π),⊙A的极坐标方程为ρ=2cosθ,点C在极轴的上方,∠AOC=