题目内容
设函数f(x)=|x2-9x+18|+x2-9x+18,则f(1)+f(2)+…+f(7)的值为 .
考点:函数的值
专题:函数的性质及应用
分析:利用绝对值性质和配方法求解.
解答:
解:∵x2-9x+18=(x-
)2-
,
由x2-9x+18=(x-
)2-
≥0,
解得x≤3或x≥6.
∴f(1)=2(1-9+18)=20,
f(2)=2(4-18+18)=8,
f(3)=2(9-27+18)=0,
f(4)=f(5)=0,
f(6)=2(36-54+18)=0,
f(7)=2(49-63+18)=8,
∴f(1)+f(2)+…+f(7)=20+8+8=36.
故答案为:36.
| 9 |
| 2 |
| 9 |
| 4 |
由x2-9x+18=(x-
| 9 |
| 2 |
| 9 |
| 4 |
解得x≤3或x≥6.
∴f(1)=2(1-9+18)=20,
f(2)=2(4-18+18)=8,
f(3)=2(9-27+18)=0,
f(4)=f(5)=0,
f(6)=2(36-54+18)=0,
f(7)=2(49-63+18)=8,
∴f(1)+f(2)+…+f(7)=20+8+8=36.
故答案为:36.
点评:本题考查函数值的求法,是基础题,解题时要认真审题,注意绝对值性质和配方法的合理运用.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
已知双曲线方程为
-
=1,则双曲线的渐近线方程为( )
| x2 |
| 9 |
| y2 |
| 3 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
| D、y=±3x |
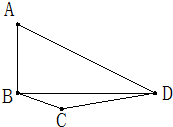 如图:平面四边形ABCD中,AB=1,∠BCD=150°,对角线BD垂直于AB且BD=2.沿BD把△ABD折起,使二面角A-BD-C为150°,则三棱锥A-BCD外接球的表面积为
如图:平面四边形ABCD中,AB=1,∠BCD=150°,对角线BD垂直于AB且BD=2.沿BD把△ABD折起,使二面角A-BD-C为150°,则三棱锥A-BCD外接球的表面积为 如图,球O内切于圆柱O1O2.记球O的体积为V1,圆柱O1O2的体积为V2,则
如图,球O内切于圆柱O1O2.记球O的体积为V1,圆柱O1O2的体积为V2,则