题目内容
若集合A={x|3≤x<7},B={x|x是非质数},C=A∩B,则C的非空子集的个数为 .
考点:交、并、补集的混合运算
专题:集合
分析:根据B为非质数,由A,以及A与B的交集为C,确定出集合C,即可求出C非空子集的个数.
解答:
解:∵A={x|3≤x<7},B={x|x是非质数},且C=A∩B,
∴C={4,6},
则C的非空子集的个数为22-1=3.
故答案为:3.
∴C={4,6},
则C的非空子集的个数为22-1=3.
故答案为:3.
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
中国古代数学著作《九章算法》中的“更相减损术”可用来求两个正整数的最大公约数.现应用此法求168与93的最大公约数:记(168,93)为初始状态,则第一步可得(75,93),第二步得到(75,18),….以上解法中,不会出现的状态是( )
| A、(57,18) |
| B、(3,18) |
| C、(6,9) |
| D、(3,3) |
在20瓶饮料中,有4瓶已过了保质期.从这20瓶饮料中任取1瓶,取到已过保质期饮料的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
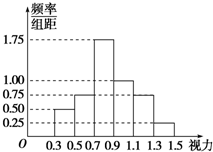 从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中视力情况进行统计,按视力分六组(0.3,0.5],(0.5,0.7],(0.7,0.9],(0.9,1.1](1.1,1.3],(1.3,1.5].其结果的频率分布直方图如图所示:若某高校A专业对视力的要求在0.9以上,则该班学生中能报A专业的人数为
从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中视力情况进行统计,按视力分六组(0.3,0.5],(0.5,0.7],(0.7,0.9],(0.9,1.1](1.1,1.3],(1.3,1.5].其结果的频率分布直方图如图所示:若某高校A专业对视力的要求在0.9以上,则该班学生中能报A专业的人数为