题目内容
设集合A={（x1，x2，x3，x4）|xi∈{0，1，-1}，i=1，2，3，4}，则A中满足条件“|x1+x2+x3+x4|=3”的元素个数为 ．
考点：元素与集合关系的判断
专题：集合
分析：由“|x1+x2+x3+x4|=3”，结合xi的取值，讨论xi所有取值的可能性，求出A中满足条件的元素个数是多少．
解答：
解：根据题意，∵“|x1+x2+x3+x4|=3”，
xi∈{0，1，-1}，i=1，2，3，4；
∴xi中有3个1和1个0，或3个-1和1个0，共有
•
+
•
=8；
∴A中满足条件的元素个数是8．
故答案为：8．
xi∈{0，1，-1}，i=1，2，3，4；
∴xi中有3个1和1个0，或3个-1和1个0，共有
| C | 3 4 |
| C | 1 1 |
| C | 3 4 |
| C | 1 1 |
∴A中满足条件的元素个数是8．
故答案为：8．
点评：本题通过集合的概念，考查了排列组合的应用问题，解题时应深刻理解题意，抓住问题的关键，进行解答问题，是基础题．
练习册系列答案
相关题目
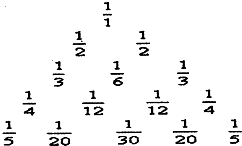如图所示的三角形数阵叫”莱布尼兹调和三角形”，它们是由整数的倒数组成的，第n行有死个数且两端的数均为告（砖≥2），每个数是它下一行左右相邻两数的和，如