题目内容
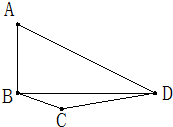 如图:平面四边形ABCD中,AB=1,∠BCD=150°,对角线BD垂直于AB且BD=2.沿BD把△ABD折起,使二面角A-BD-C为150°,则三棱锥A-BCD外接球的表面积为
如图:平面四边形ABCD中,AB=1,∠BCD=150°,对角线BD垂直于AB且BD=2.沿BD把△ABD折起,使二面角A-BD-C为150°,则三棱锥A-BCD外接球的表面积为考点:球的体积和表面积,球内接多面体
专题:综合题,空间位置关系与距离
分析:设△BCD的外接球的球心为O′,三棱锥A-BCD外接球的球心为O,求出OO′=
,△BCD的外接圆的半径,可得三棱锥A-BCD外接球的半径,即可求得结论.
| 1 |
| 4 |
解答:
解:由题意,设△BCD的外接球的球心为O′,三棱锥A-BCD外接球的球心为O,则
∵AB=1,二面角A-BD-C为150°,
∴A到平面BCD的距离为
,
∴OO′=
,
设△BCD的外接圆的半径为r,则2r=
=4,
∴r=2,
∴三棱锥A-BCD外接球的半径为
,
∴三棱锥A-BCD外接球的表面积为4π(4+
)=
.
故答案为:
.
∵AB=1,二面角A-BD-C为150°,
∴A到平面BCD的距离为
| 1 |
| 2 |
∴OO′=
| 1 |
| 4 |
设△BCD的外接圆的半径为r,则2r=
| BD |
| sin150° |
∴r=2,
∴三棱锥A-BCD外接球的半径为
4+
|
∴三棱锥A-BCD外接球的表面积为4π(4+
| 1 |
| 16 |
| 65π |
| 4 |
故答案为:
| 65π |
| 4 |
点评:本题考查的知识点是球的体积和表面积,其中根据已知条件求出球的半径是解答本题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
有一长为1km的斜坡,它的倾斜角为20°,现要将倾斜角改为10°,则坡底要加长( )
| A、0.5km | ||||
| B、1km | ||||
| C、1.5km | ||||
D、
|
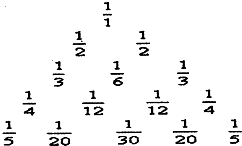 如图所示的三角形数阵叫”莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有死个数且两端的数均为告(砖≥2),每个数是它下一行左右相邻两数的和,如
如图所示的三角形数阵叫”莱布尼兹调和三角形”,它们是由整数的倒数组成的,第n行有死个数且两端的数均为告(砖≥2),每个数是它下一行左右相邻两数的和,如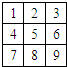 用红、黄、蓝三种颜色去涂题图中标号为1,2,…,9的9个小正方形,使得任意相邻(有公共边)的小正方形所涂的颜色不同,且“3、5、7”号数字涂色相同,则符合条件的所有涂法种数为( )
用红、黄、蓝三种颜色去涂题图中标号为1,2,…,9的9个小正方形,使得任意相邻(有公共边)的小正方形所涂的颜色不同,且“3、5、7”号数字涂色相同,则符合条件的所有涂法种数为( )