题目内容
函数f(x)=cos(πx)与函数g(x)=|log2|x-1||的图象所有交点的横坐标之和为 .
考点:函数的图象与图象变化
专题:函数的性质及应用
分析:由两函数图象的对称性知道,它们的交点也有对称性,再研究对称轴右边的交点个数,得到所求答案.
解答:
解:设P(x0,y0)是函数g(x)=|log2|x-1||的图象上任一点,
则当x=2-x0时,y=|log2|(2-x0)-1||=|log2|x0-1||=y0
∴点Q(2-x0,y0)也在函数g(x)=|log2|x-1||的图象上.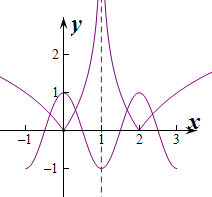
由于点P、Q关于直线x=1对称,
∴函数g(x)=|log2|x-1||的图象关于直线x=1对称.
当x=1时,函数f(x)=cos(πx)=cosπ=-1
∴函数f(x)=cos(πx)的图象关于直线x=1对称.
∴函数f(x)=cos(πx)与函数g(x)=|log2|x-1||的图象的交点关于直线x=1对称.
当1<x<2时,函数f(x)=cos(πx)单调递增,f(1)=-1,f(2)=1;
而函数g(x)=|log2|x-1||=-log2(x-1)单调递减,g(2)=0,
故在区间(1,2)内,函数f(x)=cos(πx)与函数g(x)=|log2|x-1||的图象有且只一个交点;
当2≤x≤3时,函数f(x)=cos(πx)单调递减,f(2)=1,f(3)=-1,
而函数g(x)=|log2|x-1||=log2(x-1)单调递增,g(2)=0,
故在区间(2,3)内,函数f(x)=cos(πx)与函数g(x)=|log2|x-1||的图象有且只一个交点;
当x>3时,g(x)=|log2|x-1||=log2(x-1)>1,而函数f(x)=cos(πx)≤1,
故在区间(3,+∞)内,函数f(x)=cos(πx)与函数g(x)=|log2|x-1||的图象无交点.
综上所述,函数f(x)=cos(πx)与函数g(x)=|log2|x-1||的图象共有4个交点,关于直线x=1对称,
∴函数f(x)=cos(πx)与函数g(x)=|log2|x-1||的图象所有交点的横坐标之和为4.
则当x=2-x0时,y=|log2|(2-x0)-1||=|log2|x0-1||=y0
∴点Q(2-x0,y0)也在函数g(x)=|log2|x-1||的图象上.

由于点P、Q关于直线x=1对称,
∴函数g(x)=|log2|x-1||的图象关于直线x=1对称.
当x=1时,函数f(x)=cos(πx)=cosπ=-1
∴函数f(x)=cos(πx)的图象关于直线x=1对称.
∴函数f(x)=cos(πx)与函数g(x)=|log2|x-1||的图象的交点关于直线x=1对称.
当1<x<2时,函数f(x)=cos(πx)单调递增,f(1)=-1,f(2)=1;
而函数g(x)=|log2|x-1||=-log2(x-1)单调递减,g(2)=0,
故在区间(1,2)内,函数f(x)=cos(πx)与函数g(x)=|log2|x-1||的图象有且只一个交点;
当2≤x≤3时,函数f(x)=cos(πx)单调递减,f(2)=1,f(3)=-1,
而函数g(x)=|log2|x-1||=log2(x-1)单调递增,g(2)=0,
故在区间(2,3)内,函数f(x)=cos(πx)与函数g(x)=|log2|x-1||的图象有且只一个交点;
当x>3时,g(x)=|log2|x-1||=log2(x-1)>1,而函数f(x)=cos(πx)≤1,
故在区间(3,+∞)内,函数f(x)=cos(πx)与函数g(x)=|log2|x-1||的图象无交点.
综上所述,函数f(x)=cos(πx)与函数g(x)=|log2|x-1||的图象共有4个交点,关于直线x=1对称,
∴函数f(x)=cos(πx)与函数g(x)=|log2|x-1||的图象所有交点的横坐标之和为4.
点评:本题考查了函数图象的对称性和根的存在性,利用函数单调性研究根的存在情况,利用对称性求出相应横坐标之和.本题有一定的难度,属于中档题.

练习册系列答案
相关题目
一列火车在平直的铁轨上行驶,由于遇到紧急情况,火车以速度v(t)=5-t+
(t的单位:s,v的单位:m/s)紧急刹车至停止,在此期间火车继续行驶的距离是( )
| 55 |
| 1+t |
| A、55ln10 |
| B、55ln11 |
| C、12+55ln7 |
| D、12+55ln6 |
四边形OABC中,
=
,若
=
,
=
,则
=( )
| CB |
| 1 |
| 2 |
| OA |
| OA |
| a |
| OC |
| b |
| AB |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|