题目内容
14.已知函数f(x)=$\left\{\begin{array}{l}{\frac{lnx}{x},x≥1}\\{-{x}^{3}+1,x<1}\end{array}\right.$,若关于x的方程f(x)=k有三个不同的实根,则实数k的取值范围是( )| A. | (0,$\frac{1}{e}$) | B. | (-∞,0] | C. | (-∞,$\frac{1}{e}$) | D. | [$\frac{1}{e}$,+∞) |
分析 判断f(x)的单调性,计算极值,作出f(x)的函数图象,根据图象得出k的范围.
解答 解:当x≥1时,f′(x)=$\frac{1-lnx}{{x}^{2}}$,
∴当1≤x≤e时,f′(x)≥0,当x>e时,f′(x)<0,
∴f(x)在[1,e)上单调递增,在[e,+∞)上单调递减,
∴当x=e时,f(x)取得极大值f(e)=$\frac{1}{e}$.
又f(1)=0,当x>1时,f(x)=$\frac{lnx}{x}$>0,
当x<1时,f(x)=-x3+1为减函数,
作出f(x)的大致函数图象如图所示: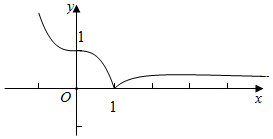
∴当0<k<$\frac{1}{e}$时,f(x)=k有3个不同的实数根.
故选A.
点评 本题考查了函数单调性判断,函数零点与函数图象的关系,属于中档题.

练习册系列答案
相关题目
5.数列{an}中,an+1=2+$\sqrt{4{a}_{n}-{{a}_{n}}^{2}}$,则a1+a2018的最大值为( )
| A. | 2 | B. | 4 | C. | 4-2$\sqrt{2}$ | D. | 4+2$\sqrt{2}$ |
2.(1+2x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则a0+a2+a4=( )
| A. | 243 | B. | 242 | C. | 121 | D. | 120 |
9.五个人排成一排,其中甲、乙两人必须排在一起,丙、丁两人不能排在一起,则不同的排法共有( )
| A. | 48种 | B. | 24种 | C. | 20种 | D. | 12种 |
6.在极坐标系中,圆ρ=2cosθ的圆心的极坐标是( )
| A. | (1,$\frac{π}{2}$) | B. | (1,-$\frac{π}{2}$) | C. | (1,π) | D. | (1,0) |
3. 已知函数f(x)及其导函数f′(x)的图象为图中四条光滑曲线中的两条,则f(x)的递增区间为( )
已知函数f(x)及其导函数f′(x)的图象为图中四条光滑曲线中的两条,则f(x)的递增区间为( )
 已知函数f(x)及其导函数f′(x)的图象为图中四条光滑曲线中的两条,则f(x)的递增区间为( )
已知函数f(x)及其导函数f′(x)的图象为图中四条光滑曲线中的两条,则f(x)的递增区间为( )| A. | (1,+∞) | B. | (-∞,2) | C. | (0,+∞) | D. | ($\frac{1}{2}$,+∞) |