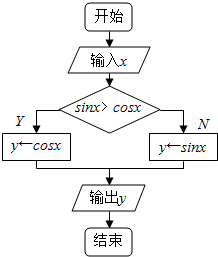
题目内容
1.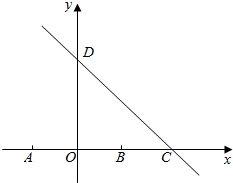 已知点A(-1,0),B(1,0),直线l:x+y=2交x轴于点C,交y轴于点D
已知点A(-1,0),B(1,0),直线l:x+y=2交x轴于点C,交y轴于点D(1)若点P是线段CD上的任意一点,求$\overrightarrow{PA}$•$\overrightarrow{PB}$的取值范围;
(2)若点P是直线l上的任意一点,求|PA|+|PB|的最小值,以及取到最小值时点P的坐标.
分析 (1)根据题意,设出点P(x,y),x∈[0,2];利用坐标表示出$\overrightarrow{PA}$•$\overrightarrow{PB}$,再利用函数的性质求出$\overrightarrow{PA}$•$\overrightarrow{PB}$的取值范围;
(2)根据题意,求出点A关于直线l的对称点A′,连接BA′交直线l于点P,|PA|+|PB|的最小值为|BA′|
解答 解:(1)∵点A(-1,0),B(1,0),直线l:x+y=2交x轴于点C,交y轴于点D;
设点P(x,y),x∈[0,2];
∴$\overrightarrow{PA}$=(-1-x,-y),$\overrightarrow{PB}$=(1-x,-y),
∴$\overrightarrow{PA}$•$\overrightarrow{PB}$=(-1-x)(1-x)+y2=x2+y2-1=x2+(2-x)2-1=2(x-1)2+1,
当x∈[0,2]时,1≤2(x-1)2+1≤3,
∴$\overrightarrow{PA}$•$\overrightarrow{PB}$的取值范围是[1,3];
(2)设A(-1,0)关于直线l:x+y=2的对称点为A′(m,n),
则$\left\{\begin{array}{l}{\frac{n}{m+1}•(-1)=-1}\\{\frac{m-1}{2}+\frac{n}{2}=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=2}\\{n=3}\end{array}\right.$,
即A′(2,3);
连接BA′交直线l于点P,
则|PA|+|PB|的最小值为|BA′|=$\sqrt{{(2-1)}^{2}{+3}^{2}}$=$\sqrt{10}$,
BA′的直线方程为$\frac{y}{3}$=$\frac{x-1}{2-1}$,
与直线l的方程联立得$\left\{\begin{array}{l}{y=3(x-1)}\\{x+y=2}\end{array}\right.$,求出点P的坐标为($\frac{5}{4}$,$\frac{3}{4}$).
点评 本题考查了点关于直线的对称点的求法以及两点间的距离公式应用问题,也考查了计算能力与转化思想的应用问题,是综合性题目.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案、选修4-4(坐标系与参数方程)、选修4-5(不等式选讲)中任选一题作答,为了了解同学们对这三道题的选做情况,王老师对他所做的甲、乙两个理科班共110人的一次数学模拟考试试卷中选做题的选题情况进行了统计,结果如下表所示:
| 选修4-1 | 选修4-4 | 选修4-5 | |
| 甲班 | 15 | x | 10 |
| 乙班 | 10 | 25 | y |
(1)求x,y的值,若把频率当成概率,分别计算两个班没选选修4-5的概率;
(2)若从甲班随机抽取2名同学,从乙班中随机抽取1名同学,对其试卷选做题得分进行分析,记3名同学中选做4-1的人数为随机变量X,求X的分布列和数学期望.
| A. | 2400种 | B. | 1500种 | C. | 400种 | D. | 60种 |