题目内容
16.2016年高考又有几个省将使用全国数学试卷,该试卷最后一题为三到选做题,即要求考生从选修4-1(几何证明选讲)、选修4-4(坐标系与参数方程)、选修4-5(不等式选讲)中任选一题作答,为了了解同学们对这三道题的选做情况,王老师对他所做的甲、乙两个理科班共110人的一次数学模拟考试试卷中选做题的选题情况进行了统计,结果如下表所示:
| 选修4-1 | 选修4-4 | 选修4-5 | |
| 甲班 | 15 | x | 10 |
| 乙班 | 10 | 25 | y |
(1)求x,y的值,若把频率当成概率,分别计算两个班没选选修4-5的概率;
(2)若从甲班随机抽取2名同学,从乙班中随机抽取1名同学,对其试卷选做题得分进行分析,记3名同学中选做4-1的人数为随机变量X,求X的分布列和数学期望.
分析 (1)由已知得$\frac{x+25}{110}$=$\frac{6}{11}$,由此能求出x,y及两个班没选选修4-5的概率.
(2)由题意学生选做4-1的概率p=$\frac{15+10}{110}$=$\frac{5}{22}$,X~B(3,$\frac{5}{22}$),由此能求出X的分布列和EX.
解答 解:(1)∵从110名学生中随机抽取一名,他选择选修4-4的概率为$\frac{6}{11}$,
∴$\frac{x+25}{110}$=$\frac{6}{11}$,解得x=60-25=35,
∴y=110-15-10-35-25-10=15.
∴两个班没选选修4-5的概率p=1-$\frac{10+15}{110}$=$\frac{17}{22}$.
(2)由题意学生选做4-1的概率p=$\frac{15+10}{110}$=$\frac{5}{22}$,
由题意知X的可能取值为0,1,2,3,且X~B(3,$\frac{5}{22}$),
P(X=0)=${C}_{3}^{0}(\frac{17}{22})^{3}$=$\frac{4913}{10648}$,
P(X=1)=${C}_{3}^{1}(\frac{5}{22})(\frac{17}{22})^{2}$=$\frac{4335}{10648}$,
P(X=2)=${C}_{3}^{2}(\frac{5}{22})^{2}(\frac{17}{22})$=$\frac{1275}{10648}$,
P(X=3)=${C}_{3}^{3}(\frac{5}{22})^{3}$=$\frac{125}{10648}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{4913}{10648}$ | $\frac{4335}{10648}$ | $\frac{1275}{10648}$ | $\frac{125}{10648}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,注意二项分布的性质的合理运用.

| A. | [$\frac{15}{8}$,+∞) | B. | [3,+∞) | C. | [$\frac{9}{4}$,+∞) | D. | ($\sqrt{5}$,+∞) |
| A. | [$\frac{1}{2}$,+∞) | B. | [$\frac{2}{3}$,+∞) | C. | (1,+∞) | D. | [1,+∞) |
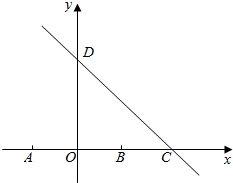 已知点A(-1,0),B(1,0),直线l:x+y=2交x轴于点C,交y轴于点D
已知点A(-1,0),B(1,0),直线l:x+y=2交x轴于点C,交y轴于点D