题目内容
6.如图,若输入的x值为$\frac{π}{3}$,则相应输出的值为$\frac{1}{2}$.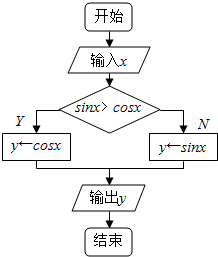
分析 根据题意得出执行程序框图后输出的是分段函数y=$\left\{\begin{array}{l}{y=cosx,sinx>cosx}\\{y=sinx,sinx≤cosx}\end{array}\right.$,由此求出输入x=$\frac{π}{3}$时输出y的值.
解答 解:根据题意,执行程序框图后输出的是分段函数
y=$\left\{\begin{array}{l}{y=cosx,sinx>cosx}\\{y=sinx,sinx≤cosx}\end{array}\right.$,
当输入x=$\frac{π}{3}$时,sin$\frac{π}{3}$>cos$\frac{π}{3}$,
所以输出的y=cos$\frac{π}{3}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了选择语句的应用问题,是基础题目.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
16.已知函数f(x)=x3+x-16.
(1)求满足斜率为4的曲线的切线方程;
(2)求曲线y=f(x)在点(2,-6)处的切线的方程;
(3)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程.
(1)求满足斜率为4的曲线的切线方程;
(2)求曲线y=f(x)在点(2,-6)处的切线的方程;
(3)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程.
16.已知函数f(x)=$\left\{\begin{array}{l}{a{x}^{2}+1,x≥0}\\{(a-1){e}^{x},x<0}\end{array}\right.$在(-∞,+∞)上是单调函数,则实数a的取值范围是( )
| A. | (1,2] | B. | [2,+∞) | C. | [-2,-1)∪[2,+∞) | D. | (-∞,-2]∪(1,2) |
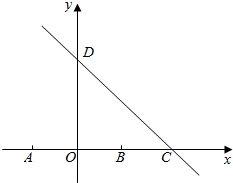 已知点A(-1,0),B(1,0),直线l:x+y=2交x轴于点C,交y轴于点D
已知点A(-1,0),B(1,0),直线l:x+y=2交x轴于点C,交y轴于点D