题目内容
10.某大学进行自主招生考试面试,需将每5位考生组成一组进行口头答题,每位考生可以从5个备选题目中任选1题口头作答,则恰有2个题目没有被某组5为考生选中的情况有( )| A. | 2400种 | B. | 1500种 | C. | 400种 | D. | 60种 |
分析 先从5道题种选2道,则其余3道必须有人选,把5位考生可以分为(3,1,1)和(2,2,1)两组,分组再分配到三道题种,问题得以解决.
解答 解:先从5道题种选2道,则其余3道必须有人选,把5位考生可以分为(3,1,1)和(2,2,1)两组,
分组的种数为:C53+$\frac{{C}_{5}^{2}•{C}_{3}^{2}}{{A}_{2}^{2}}$=25种,
故有C53•25•A33=1500Z种,
故选:B.
点评 本题考查分步计数原理以及分组分配的问题,关键是分组,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知函数f(x)=x-$\frac{1}{x+1}$,g(x)=x2-2ax+4,若任意x1∈[0,1],存在x2∈[1,2],使f(x1)≥g(x2),则实数a的取值范围是( )
| A. | [$\frac{15}{8}$,+∞) | B. | [3,+∞) | C. | [$\frac{9}{4}$,+∞) | D. | ($\sqrt{5}$,+∞) |
20.已知集合A={x|x2-2x-3≤0},B={x|x>2},则A∩(∁RB)等于( )
| A. | (1,2) | B. | (1,2] | C. | [-1,2) | D. | [-1,2] |
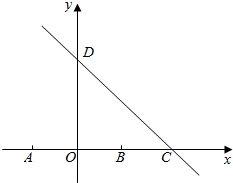 已知点A(-1,0),B(1,0),直线l:x+y=2交x轴于点C,交y轴于点D
已知点A(-1,0),B(1,0),直线l:x+y=2交x轴于点C,交y轴于点D