题目内容
11.已知$\overrightarrow a$=(1,0),$\overrightarrow b$=(2,1).(I)求|${\overrightarrow a$+3$\overrightarrow b}$|;
(II)当k为何值时,k$\overrightarrow a$-$\overrightarrow b$与$\overrightarrow a$+3$\overrightarrow b$平行,并说明平行时它们是同向还是反向?
分析 (Ⅰ)先求出$\overrightarrow{a}+3\overrightarrow{b}$=(7,3),由此能求出$|{\overrightarrow a+3\overrightarrow b}|$.
(Ⅱ)先求出$k\overrightarrow a-\overrightarrow b$=(k-2,-1),$\overrightarrow a+3\overrightarrow b$=(7,3),再由$k\overrightarrow a-\overrightarrow b$与$\overrightarrow a+3\overrightarrow b$平行,能求出结果.
解答 解:(Ⅰ)∵$\overrightarrow a=(1,0)$,$\overrightarrow b=(2,1)$,
∴$\overrightarrow{a}+3\overrightarrow{b}$=(7,3),
∴$|{\overrightarrow a+3\overrightarrow b}|$=$\sqrt{49+9}$=$\sqrt{58}$.
(Ⅱ)∵$k\overrightarrow a-\overrightarrow b$=(k-2,-1),$\overrightarrow a+3\overrightarrow b$=(7,3),
又$k\overrightarrow a-\overrightarrow b$与$\overrightarrow a+3\overrightarrow b$平行,
∴3(k-2)=-7,∴$k=-\frac{1}{3}$,
此时-$\frac{1}{3}\overrightarrow{a}-\overrightarrow{b}$=(-$\frac{7}{3}$,-1),$\overrightarrow{a}+3\overrightarrow{b}$=-3(-$\frac{1}{3}\overrightarrow{a}-\overrightarrow{b}$),
∴当$k=-\frac{1}{3}$时 反向共线.
点评 本题考查向量的模的求法,考查实数值的求法及向量同向或反向的判断,是基础题,解题时要认真审题,注意向量坐标运算的合理运用.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案| A. | $\frac{1}{7}$ | B. | 0 | C. | $-\frac{1}{4}$ | D. | -3 |
(1)求满足斜率为4的曲线的切线方程;
(2)求曲线y=f(x)在点(2,-6)处的切线的方程;
(3)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程.
| A. | g(x)=$\sqrt{x}$-1 | B. | g(x)=2x-1 | C. | $g(x)=ln({x-\frac{1}{2}})$ | D. | g(x)=4x-1 |
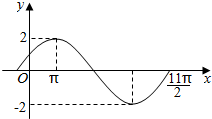 已知函数$f(x)=Asin(ωx+\frac{π}{6})(A>0,ω>0)$)图象的一部分如图所示.
已知函数$f(x)=Asin(ωx+\frac{π}{6})(A>0,ω>0)$)图象的一部分如图所示.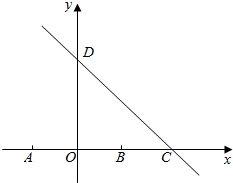 已知点A(-1,0),B(1,0),直线l:x+y=2交x轴于点C,交y轴于点D
已知点A(-1,0),B(1,0),直线l:x+y=2交x轴于点C,交y轴于点D