题目内容
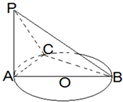 如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中直角三角形的个数为( )
如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆周上不同于A、B的任意一点,则图中直角三角形的个数为( )| A、1 | B、2 | C、3 | D、4 |
考点:直线与平面垂直的性质
专题:空间位置关系与距离
分析:利用直径所对的圆周角为直角和线面垂直的判定定理和性质定理即可判断出答案.
解答:
解:AB是圆O的直径,则AC⊥BC,
由于PA⊥平面ABC,
则PA⊥BC,
即有BC⊥平面PAC,
则有BC⊥PC,则△PBC是直角三角形;
由于PA⊥平面ABC,则PA⊥AB,PA⊥AC,则△PAB和△PAC都是直角三角形;
再由AC⊥BC,得∠ACB=90°,则△ACB是直角三角形.
综上可知:此三棱锥P-ABC的四个面都是直角三角形.
故选D.
由于PA⊥平面ABC,
则PA⊥BC,
即有BC⊥平面PAC,
则有BC⊥PC,则△PBC是直角三角形;
由于PA⊥平面ABC,则PA⊥AB,PA⊥AC,则△PAB和△PAC都是直角三角形;
再由AC⊥BC,得∠ACB=90°,则△ACB是直角三角形.
综上可知:此三棱锥P-ABC的四个面都是直角三角形.
故选D.
点评:熟练掌握直径所对的圆周角的性质、线面垂直的判定和性质定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设函数f(x)=x2─2,用二分法求f(x)=0的一个近似解时,第1步确定了一个区间为(1,
),到第3步时,求得的近似解所在的区间应该是( )
| 3 |
| 2 |
A、(1,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
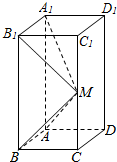 如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点.
如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点.