Question

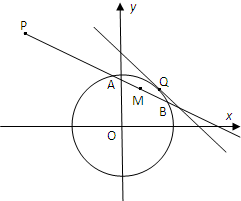过点P（-4，4）作直线l与圆O：x²+y²=4相交于A、B两点．
（Ⅰ）若直线l变动时，求AB中点M的轨迹方程；
（Ⅱ）若直线l的斜率为-

1

2

，求弦AB的长；
（Ⅲ）若一直线与圆O相 切于点Q且与x轴的正半轴，y轴的正半轴围成一个三角形，当该三角形面积最小时，求点Q的坐标．

Answer 1

考点：轨迹方程

专题：综合题,直线与圆

分析：（Ⅰ）点M所在曲线是以OP为直径的圆，可得AB中点M的轨迹方程；
（Ⅱ）求出直线l的方程是：y-4=-

1

2

（x+4），可得点O到直线l的距离，即可求弦AB的长；
（Ⅲ）求出两个坐标轴的正半轴于切线围成的三角形面积，利用基本不等式可得该三角形面积最小时，点Q的坐标．

解答： 解：（Ⅰ）因为点M是AB的中点，所以OM⊥AB，
则点M所在曲线是以OP为直径的圆，其方程为x（x+4）+y（y-4）=0，
即（x+2）²+（y-2）²=8；                                  …（4分）
（Ⅱ）因为直线l的斜率为-

1

2

，所以直线l的方程是：y-4=-

1

2

（x+4），
即x+2y-4=0，…（6分）
设点O到直线l的距离为d，则d=

4

5

，
所以AB=2

4- 16 5

=

4 5

5

；       …（10分）
（Ⅲ）设切点Q的坐标为（x₀，y₀）（x₀＞0，y₀＞0）．则切线斜率为-

x0

y0

．
所以切线方程为y-y₀=-

x0

y0

（x-x₀）．
又x₀²+y₀²=4，则x₀x+y₀y=4         …（12分）
此时，两个坐标轴的正半轴于切线围成的三角形面积S=

1

2

•

4

x0

•

4

y0

=

8

x0y0

．…（14分）
由x₀²+y₀²=4≥2x₀y₀，知当且仅当x₀=y₀=

2

时，x₀y₀有最大值．
即S有最小值．因此点Q的坐标为（

2

，

2

）．             …（16分）

点评：本题考查圆的方程，考查直线与圆的位置关系，考察基本不等式的运用，属于中档题．