题目内容
18.已知函数f(x)=2+log${\;}_{\frac{1}{2}}$x.(I)请画出函数的草图;
(Ⅱ)当x=$\frac{1}{4}$时,求f(x)的值;
(Ⅲ)当-1<f(x)≤3时,求x的取值范围.
分析 (I)根据对数函数的图象和性质,结合函数图象的平移变换,可得函数f(x)=2+log${\;}_{\frac{1}{2}}$x的草图;
(Ⅱ)将x=$\frac{1}{4}$代入,可得答案;
(Ⅲ)当-1<f(x)≤3时,-1<2+log${\;}_{\frac{1}{2}}$x≤3,解得答案.
解答 解:(I)函数f(x)=2+log${\;}_{\frac{1}{2}}$x的草图如下图所示:
(Ⅱ)当x=$\frac{1}{4}$时,f($\frac{1}{4}$)=2+log${\;}_{\frac{1}{2}}$$\frac{1}{4}$=4.
(Ⅲ)当-1<f(x)≤3时,-1<2+log${\;}_{\frac{1}{2}}$x≤3,
即-3<log${\;}_{\frac{1}{2}}$x≤1,
即$\frac{1}{2}$≤x<8.
点评 本题考查的知识点是对数函数的图象和性质,熟练掌握对数函数的图象和性质,是解答的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
13.已知函数$f(x)=\sqrt{3}sin(π-x)cos(-x)+sin(π+x)cos(\frac{π}{2}-x)$图象上的一个最低点为A,离A最近的两个最高点分别为B与C,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=( )
| A. | $9+\frac{π^2}{9}$ | B. | $9-\frac{π^2}{9}$ | C. | $4+\frac{π^2}{4}$ | D. | $4-\frac{π^2}{4}$ |
7.已知椭圆的焦点为F1(0,-1),F2(0,1),且经过点M($\frac{7}{4}$,$\frac{3\sqrt{2}}{2}$),则椭圆的方程为( )
| A. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | B. | $\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1 | C. | $\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{8}$=1 | D. | $\frac{{x}^{2}}{7}$+$\frac{{y}^{2}}{8}$=1 |
8.已知椭圆C1:$\frac{{x}^{2}}{{{a}_{1}}^{2}}$+$\frac{{y}^{2}}{{{b}_{1}}^{2}}$=1(a1>b1>0)与双曲线C2:$\frac{{x}^{2}}{{{a}_{2}}^{2}}$-$\frac{{y}^{2}}{{{b}_{2}}^{2}}$=1(a2>0,b2>0)有相同的焦点F1,F2,设椭圆的离心率为e1,双曲线的离心率为e2,O为坐标原点,P是两曲线的公共点,且∠F1PF2=60°,则$\frac{{e}_{1}{e}_{2}}{\sqrt{3{{e}_{1}}^{2}+{{e}_{2}}^{2}}}$的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 1 |
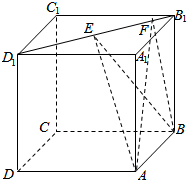 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{1}{2}$,则下列结论中正确的序号是①②③.
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{1}{2}$,则下列结论中正确的序号是①②③.