题目内容
13.已知函数$f(x)=\sqrt{3}sin(π-x)cos(-x)+sin(π+x)cos(\frac{π}{2}-x)$图象上的一个最低点为A,离A最近的两个最高点分别为B与C,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=( )| A. | $9+\frac{π^2}{9}$ | B. | $9-\frac{π^2}{9}$ | C. | $4+\frac{π^2}{4}$ | D. | $4-\frac{π^2}{4}$ |
分析 由三角函数公式化简可得f(x)=sin(2x+$\frac{π}{6}$)-$\frac{1}{2}$,结合图象可得A、B、C的坐标,可得向量的坐标,计算可得.
解答 解:由三角函数公式化简可得f(x)=$\sqrt{3}$sinxcosx-sinxsinx
=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$(1-cos2x)=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x-$\frac{1}{2}$
=sin(2x+$\frac{π}{6}$)-$\frac{1}{2}$,令2x+$\frac{π}{6}$=$\frac{3π}{2}$可得x=$\frac{2π}{3}$,
可取一个最低点A($\frac{2π}{3}$,-$\frac{3}{2}$),
同理可得B($\frac{π}{6}$,$\frac{1}{2}$),C($\frac{7π}{6}$,$\frac{1}{2}$),
∴$\overrightarrow{AB}$=(-$\frac{π}{2}$,2),$\overrightarrow{AC}$=($\frac{π}{2}$,2),
∴$\overrightarrow{AB}$•$\overrightarrow{AC}$=-$\frac{{π}^{2}}{4}$+4,
故选:D.
点评 本题考查三角函数恒等变换,涉及图象的性质和向量的数量积的运算,属基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
3.$4{({\frac{16}{49}})^{-\frac{1}{2}}}+lg2+lg50$=( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
8.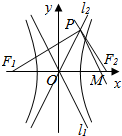 已知F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的左、右焦点,l1,l2为双曲线的两条渐近线.设过点M(b,0)且平行于l1的直线交l2于点P.若PF1⊥PF2,则该双曲线的离心率为( )
已知F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的左、右焦点,l1,l2为双曲线的两条渐近线.设过点M(b,0)且平行于l1的直线交l2于点P.若PF1⊥PF2,则该双曲线的离心率为( )
 已知F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的左、右焦点,l1,l2为双曲线的两条渐近线.设过点M(b,0)且平行于l1的直线交l2于点P.若PF1⊥PF2,则该双曲线的离心率为( )
已知F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的左、右焦点,l1,l2为双曲线的两条渐近线.设过点M(b,0)且平行于l1的直线交l2于点P.若PF1⊥PF2,则该双曲线的离心率为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{14-2\sqrt{41}}}{2}$ | D. | $\frac{\sqrt{14+2\sqrt{41}}}{2}$ |
 如图所示,AD∥BC∥EF,平面ADFE⊥平面BCFE,AE⊥EF,BE⊥EF,AD=AE=BE=2,EF=3,BC=4,G为BC的中点.
如图所示,AD∥BC∥EF,平面ADFE⊥平面BCFE,AE⊥EF,BE⊥EF,AD=AE=BE=2,EF=3,BC=4,G为BC的中点.