题目内容
完成下列各题:
(Ⅰ)求函数f(x)=
的定义域;
(Ⅱ)求函数f(x)=
的值域.
(Ⅰ)求函数f(x)=
|
(Ⅱ)求函数f(x)=
| sinx+1 |
| cosx+3 |
考点:函数的值域,函数的定义域及其求法
专题:数形结合,函数思想,函数的性质及应用
分析:(1)3-tanx≥0,解不等式得:kπ-
<x≤kπ+
,即可得到答案.
(2)运用数形结合的思想解决.
| π |
| 2 |
| π |
| 3 |
(2)运用数形结合的思想解决.
解答:
解:(1)函数f(x)=
的定义域
-tanx≥0,解不等式得:kπ-
<x≤kπ+
,k∈Z
函数f(x)=
的定义域:(kπ-
,kπ+
],k∈Z,
(2))
几何意义为:点(cosx,sinx),点(-3,-1)两点连线的斜率,点(cosx,sinx)为单位圆上的点.
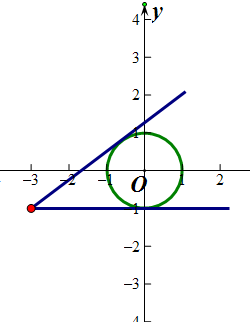
设斜率为k,则切线方程为kx-y+3k-1=0,
根据直线与圆的位置关系得:
=1,
解得:k=0,k=
,
有图形可判断:
函数f(x)=
的值域为[0,
]
|
| 3 |
| π |
| 2 |
| π |
| 3 |
函数f(x)=
|
| π |
| 2 |
| π |
| 3 |
(2))
| sinx+1 |
| cosx+3 |
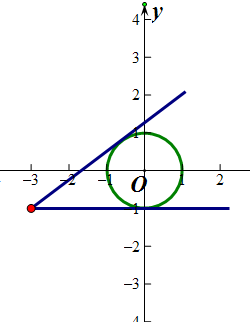
设斜率为k,则切线方程为kx-y+3k-1=0,
根据直线与圆的位置关系得:
| |3k-1| | ||
|
解得:k=0,k=
| 3 |
| 4 |
有图形可判断:
函数f(x)=
| sinx+1 |
| cosx+3 |
| 3 |
| 4 |
点评:本题综合考查了不等式在求解定义域中的运用,运用数形结合的思想求解函数值域.

练习册系列答案
相关题目
下列函数中,满足“f(x+y)=f(x)f(y)”的单调递增函数是( )
A、f(x)=x
| ||
| B、f(x)=x3 | ||
C、f(x)=(
| ||
| D、f(x)=3x |
下列四组中的f(x),g(x),表示同一个函数的是( )
| A、f(x)=1,g(x)=x0 | ||
B、f(x)=x-1,g(x)=
| ||
C、f(x)=x,g(x)=(
| ||
D、f(x)=|1-2x|,g(x)=
|