Question

某桥的桥洞呈抛物线形，桥下水面宽16m，当水面上涨2m时，水面宽变为12m，此时桥洞顶部距水面高度为多少米？

Answer 1

考点：抛物线的简单性质

专题：圆锥曲线的定义、性质与方程

分析：先根据题目条件建立直角坐标系，设出抛物线的方程，然后利用点在曲线上，确定方程，求得点的坐标，也就得到水面的宽．

解答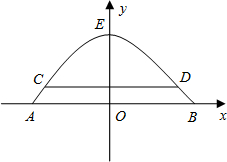： 解：如图建立直角坐标系
设抛物线y=ax²+c，由题意可知抛物线过点（6，2），（8，0）．
所以

36a+c=2 64a+c=0

解得a=-

1

14

，c=

32

7

；
所以抛物线解析式为y=-

1

14

x2+

32

7

，
令x=0，得y=

32

7

；
所以当水面上涨2m时，水面宽变为12m，此时桥洞顶部距水面高度为

32

7

-2=

18

7

米．

点评：本题考查了抛物线的应用，以及待定系数法求方程，注意点在曲线上，则点的坐标满足解析式，注意：建坐标系不同，解析式不同，属于基础题，