Question

如图，已知点H在正方体ABCD-A₁B₁C₁D₁的对角线B₁D₁上，∠HDA=60°．
（Ⅰ）求DH与CC₁所成角的大小；
（Ⅱ）求DH与平面A₁BD所成角的正弦值．

Answer 1

考点：直线与平面所成的角,异面直线及其所成的角

专题：综合题,空间角

分析：（Ⅰ）建立空间直角坐标系，设H（m，m，1）（m＞0），求出

CC1

、

DH

，利用向量的夹角公式可求DH与CC′所成角的大小；
（Ⅱ）求出平面A₁BD的法向量，利用向量的夹角公式，即可得出结论．

解答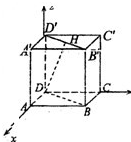： 解：（Ⅰ）建立如图所示的坐标系，设H（m，m，1）（m＞0），
则

DA

=（1，0，0），

CC1

=（0，0，1），连接BD，B₁D₁．
则

DH

=（m，m，1）（m＞0），
由已知＜

DA

，

DH

＞=60°，∴可得2m=

2m2+1

，解得m=

2

2

，
∴

DH

=（

2

2

，

2

2

，1），
∴cos＜

DA

，

CC1

＞=

2

2

，
∴＜

DA

，

CC1

＞=45°，即DH与CC′所成角的大小为45°；
（Ⅱ）设平面A₁BD的法向量为

n

=（x，y，z），则

x+z=0 x+y=0

令x=1得

n

=（1，-1，-1）是平面A₁BD的一个法向量．…（9分）
设DH与平面A₁BD所成的角为θ，
∴sinθ=cos＜

DH

，

n

＞=-

6

6

．…（12分

点评：本题考查向量知识的运用，考查空间角，正确运用向量的夹角公式是关键．