题目内容
下列命题中的假命题是( )
| A、?x∈R,21-x>0 | ||
| B、?x0∈R,当x>x0时,恒有1.1x<x4 | ||
C、?x∈(0,+∞),2x>x
| ||
| D、?α∈R,使函数 y=xα的图象关于y轴对称 |
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:本题考查特称命题、全程命题的真假判断和常见函数的性质,A中为指数类型的函数,必大于0;B、C比较指数函数比幂函数的增长快,故B假C真;D考察幂函数中的五大类代表函数,不妨令y=x2.
解答:
 解:A、x∈R,1-x∈R,21-x>0,为真命题;
解:A、x∈R,1-x∈R,21-x>0,为真命题;
B、令f(x)=1.1x,为指数函数;g(x)=x4,为幂函数,指数函数增长要快于幂函数,则命题为假
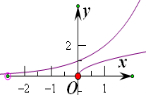
C、?x∈(0,+∞),2x>x
,令f(x)=2x,g(x)=x
作图,由图象可知,命题为真;
D、α∈R,不妨令α=2,函数y=x2的图象关于y轴对称,D为真命题;
故选:B.
 解:A、x∈R,1-x∈R,21-x>0,为真命题;
解:A、x∈R,1-x∈R,21-x>0,为真命题;B、令f(x)=1.1x,为指数函数;g(x)=x4,为幂函数,指数函数增长要快于幂函数,则命题为假
C、?x∈(0,+∞),2x>x
| 1 |
| 2 |
| 1 |
| 2 |
D、α∈R,不妨令α=2,函数y=x2的图象关于y轴对称,D为真命题;
故选:B.
点评:在解答B,C两个选项时,要有一个基本知识点.即几种典型的增函数.
指数函数型:y=ax,a>1,增速最快;
幂函数型:y=xα,α>0,x>0,增速次之;
对数函数型:y=logax,a>1,增速最慢.
指数函数型:y=ax,a>1,增速最快;
幂函数型:y=xα,α>0,x>0,增速次之;
对数函数型:y=logax,a>1,增速最慢.

练习册系列答案
相关题目
已知全集U={0,2,4,6,8,10},集合A={2,4,6},B={0,2,6,8},则CU(A∩B)为( )
| A、{0,8,10} |
| B、{0,4,8,10} |
| C、{10} |
| D、∅ |
在数列{an}中,a1=3,an=2an-1+n-2(n≥2,且n∈N*),下列哪一个是数列中的项( )
| A、210-10 |
| B、211-10 |
| C、212-10 |
| D、213-10 |
如图是一个几何体的三视图,则该几何体的体积是( )
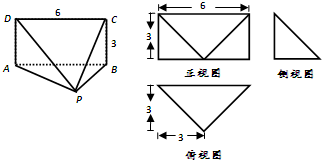

| A、54 | B、27 | C、18 | D、9 |