题目内容
19.已知两点A(0,-6),B(0,6),若圆(x-a)2+(y-3)2=4上任意一点P,都有∠APB为钝角,则实数a的取值范围是a>$\sqrt{55}$或a$<-\sqrt{55}$.分析 要使圆(x-a)2+(y-3)2=4上任意一点P,都有∠APB为钝角,则圆(x-a)2+(y-3)2=4与圆x2+y2=36外离即可.
解答 解:要使圆(x-a)2+(y-3)2=4上任意一点P,都有∠APB为钝角,
则圆(x-a)2+(y-3)2=4与圆x2+y2=36外离,即圆心距大于半径之和,
$\sqrt{{a}^{2}+{3}^{2}}>6+2$,解得a2>55,a>$\sqrt{55}$,或a$<-\sqrt{55}$.
故答案为:a>$\sqrt{55}$,或a$<-\sqrt{55}$.
点评 本题考查了圆与圆的位置关系.转化思想是解题的关键,属于中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
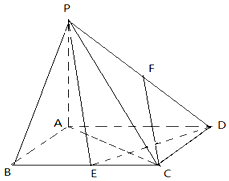 如图,四棱锥P-ABCD的底面是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E、F分别为BC与PD的中点.
如图,四棱锥P-ABCD的底面是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E、F分别为BC与PD的中点.