题目内容
4.已知函数f(x)=ex,x∈R.(1)求f(x)的图象在点(0,f(0))处的切线方程;
(2)证明:曲线y=f(x)与直线y=ex有唯一公共点.
分析 (1)求导数,确定切线的斜率、切点坐标,即可求出f(x)的图象在点(0,f(0))处的切线方程;
(2)设g(x)=ex-ex,曲线y=ex与y=ex的公共点的个数等于函数g(x)=ex-ex零点的个数.
解答 (1)解:∵f′(0)=e0=1,f(0)=1,∴切线方程为y-1=1•(x-0),即x-y+1=0.
(2)证明:设g(x)=ex-ex,曲线y=ex与y=ex的公共点的个数等于函数g(x)=ex-ex零点的个数.
∵g′(x)=ex-e,令g′(x)=0,得x=1,
∴g(x)在(-∞,1)上单调递减,在(1,+∞)上单调递增,
∴g(x)的最小值g(1)=e1-e=0,
g(x)=ex-ex≥0(仅当x=1时,等号成立).
∴曲线y=f(x)与直线y=ex有唯一公共点.
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查函数的单调性与最值,正确构造函数是关键.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
19.已知A(1,0)、B(0,1),C(x,-1),若A,B,C三点共线,则线段AC的长等于( )
| A. | $\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
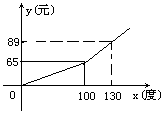 西部大部分地区的电力紧缺,电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
西部大部分地区的电力紧缺,电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题: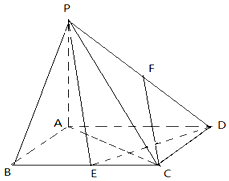 如图,四棱锥P-ABCD的底面是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E、F分别为BC与PD的中点.
如图,四棱锥P-ABCD的底面是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E、F分别为BC与PD的中点.