题目内容
5.在区间[0,1]上随机地选择三个数a,b,c,则不等式“a2+b2+c2≤1”成立的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{{\sqrt{3}π}}{9}$ | D. | $\frac{π}{6}$ |
分析 以体积为测度,计算相应的体积,即可得出结论.
解答 解:依题意得,实数a、b、c满足这样的点(a,b,c)可视为在空间直角坐标系下的单位正方体区域(其中原点是该正方体的一个顶点)内的点,其中满足|OM|≤1,的点(a,b,c)可视为在空间直角坐标系下的单位正方体区域内且还在以原点为球心、1为半径的球形区域内的点,该部分的体积恰好等于该球体积的$\frac{1}{8}•\frac{4}{3}π•{1}^{3}$=$\frac{π}{6}$,因此|OM|≤1的概率为=$\frac{π}{6}$,
故选D.
点评 本题考查几何概型,考查体积的计算,正确计算体积是关键.

练习册系列答案
相关题目
20.在△ABC中,已知b=3,c=3$\sqrt{3}$,A=30°,则边a等于( )
| A. | 9 | B. | 3 | C. | 27 | D. | 3$\sqrt{3}$ |
17.在△ABC中,AB=3,BC=4,D是BC的中点,且$∠B=\frac{π}{3}$,则sin∠ADC=( )
| A. | $\frac{{\sqrt{7}}}{4}$ | B. | $\frac{{3\sqrt{21}}}{14}$ | C. | $\frac{{\sqrt{39}}}{26}$ | D. | $\frac{{\sqrt{7}}}{28}$ |
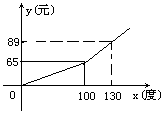 西部大部分地区的电力紧缺,电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
西部大部分地区的电力紧缺,电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题: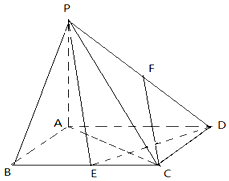 如图,四棱锥P-ABCD的底面是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E、F分别为BC与PD的中点.
如图,四棱锥P-ABCD的底面是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E、F分别为BC与PD的中点.