题目内容
2.在等差数列中,a9=3,则此数列前17项和等于( )| A. | 51 | B. | 34 | C. | 102 | D. | 不能确定 |
分析 由等差数列{an}的性质可得:a1+a17=2a9=6,再利用前n项和公式即可得出.
解答 解:由等差数列{an},a9=3,
∴a1+a17=2a9=6,
∴此数列前17项的和S17=$\frac{17({a}_{1}+{a}_{17})}{2}$=17×3=51.
故选:A.
点评 本题考查了等差数列的性质及其前n项和公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
17.在△ABC中,AB=3,BC=4,D是BC的中点,且$∠B=\frac{π}{3}$,则sin∠ADC=( )
| A. | $\frac{{\sqrt{7}}}{4}$ | B. | $\frac{{3\sqrt{21}}}{14}$ | C. | $\frac{{\sqrt{39}}}{26}$ | D. | $\frac{{\sqrt{7}}}{28}$ |
11.设函数f(x)为定义域为R的奇函数,且f(x)=f(2-x),当x∈[0,1]时,f(x)=sinx,则函数g(x)=|cos(πx)|-f(x)在区间$[-\frac{5}{2},\frac{9}{2}]$上的所有零点的和为( )
| A. | 6 | B. | 7 | C. | 13 | D. | 14 |
12.下列命题中错误的是( )
| A. | 如果平面α外的直线a不平行于平面α,平面α内不存在与a平行的直线 | |
| B. | 如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么直线l⊥平面γ | |
| C. | 如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β | |
| D. | 一条直线与两个平行平面中的一个平面相交,则必与另一个平面相交 |
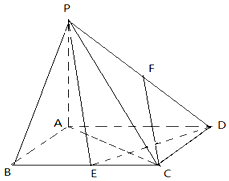 如图,四棱锥P-ABCD的底面是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E、F分别为BC与PD的中点.
如图,四棱锥P-ABCD的底面是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E、F分别为BC与PD的中点.